分析设置

软件提供四种分析类型：

• “传热分析”
• “模态分析”
• “静力/拟静力分析”
• “时程分析”

满足重力坝设计和工程安全校核需求。用户可在“分析类型”选项中切换并进入不同的分析类型，调整计算输入并进行计算。

传热分析

“传热分析”设置仅在选定“有限元法”时出现。

传热分析仅对重力坝的坝体部分进行计算。其作为单独的计算可结合气温和水温边界条件，通过求解传热方程：

$$ \lambda \Delta T(\mathbf{x}) = 0 \tag{1} $$

求解重力坝坝体温度场，其结果可作为“静力/拟静力分析”和“时程分析”的输入载荷，用于计算考虑温度情况的重力坝应力水平。

提示:

NB/T 35026-2014《混凝土重力坝设计规范》中对中、高坝采用有限元法进行温度场和温度应力分析，主要用于施工期坝体防裂和温度控制设计，坝体断面设计一般不需要考虑温度应力。

实际工程中发现，运行期坝体应力状态随气温作周期性变化，由温度变化导致的坝踵应力周期性波动幅值可达 5MPa。因此软件提供有限元热固耦合计算功能，允许用户考虑温度应力做进一步安全校核。

1. 材料

“传热分析”需定义的材料参数为：

• “坝体导热系数”$\lambda$（$W/m.K$）

“坝体导热系数”默认设置采用 GB/T 51394-2020《水工建筑物载荷标准》的建议初始混凝土导热系数：2.94 $W/m.K$。

2. 边界

“传热分析”的边界设置中，实际用于计算的“气温的年周期变化过程”和“水库坝前水温”根据《水工建筑物载荷标准》，由多个输入量计算得到，需定义的参数为：

• “月份” $\tau$

用于计算“气温”的参数：

• “年平均气温” $T_{am}$($\degree C$)
• “气温年变幅” $A_a$($\degree C$)
• “初始相位” $\tau_0$(月)

以及用于计算“水温”的参数：

• “上游水位” $H_{am}$（$m$）

• “下游水位” $H_{av}$（$m$）

• “坝前正常水深” $H_n$($m$)

• “水库变化温度层深度” $y_0$($m$)

• “太阳辐射温度增量” $\Delta_a$($\degree C$)

  仅多年调节水库需设置，当 $H_n \geq y_0$ 时参与多年平均水温年变幅的计算。

• “是否多年调节水库”

结构外界“气温的年周期变化过程”根据《水工建筑物载荷标准》，可按以下公式得到：

$$T_a=T_{am}+A_{a}\ cos\left(\omega(\tau-\tau_0)\right) \tag{2}$$

其中$T_{a}$为多年月平均气温(℃)，即坝体与空气接触表面边界温度。对于纬度高于 30° 的地区，取$\tau_0=6.5$，对于纬度低于或等于 30° 的地区，取$\tau_0=6.7$。

“水库坝前水温”根据《水工建筑物载荷标准》，可按以下公式得到：

$$T_w(y,\tau)=T_{wm}(y)+A_w(y)cos\omega[\tau-\tau_0-\varepsilon\left(y\right)] \tag{3}$$

其中:

• $T_w(y,\tau)$为坝前水深 $y$($m$)处，$\tau$ 月时刻的多年月平均水温($\degree C$)，即上游坝面水温边界。
• $T_{wm}(y)$为坝前正常水深$y$($m$)处的多年平均水温($\degree C$)
• $A_w(y)$为坝前正常水深$y$($m$)处多年平均水温年变幅($\degree C$))
• $\varepsilon\left(y\right)$为水深 𝑦($m$)处水温年周期变化过程和气温年周期变化过程的相位差

$T_w$、$T_{wm}$和 $A_w$可利用上下游水位$H_{am}$、$H_{av}$、坝前正常水位 $H_n$和水库变化温度层深度 $y_0$通过经验公式计算得到。

有限元传热仿真计算仅计算坝体区域温度场，按 $T_a$、$T_w$计算上下游坝面及坝顶气温和水温边界，坝基面温度边界按从上游坝踵到下游坝趾线性分布假设计算。

3. 计算结果

点击左边栏下方的“开始计算”按钮，软件会根据用户的参数设置进行传热学计算。计算成功后会显示“计算成功”标签。此时页面的中部会出现重力坝坝体的温度场分布云图。

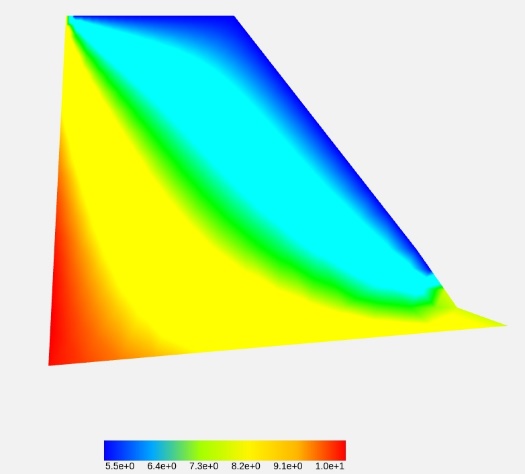
云图的颜色代表各位置的温度，单位为 $\degree C$，数值对应云图下方的刻度条。

模态分析

“模态分析”分析类型仅在求解方法选定“有限元法”时出现。其作为单独的计算可分析重力坝和坝基结构的振动特性，其结果可作为“时程分析”的基础，用于减少计算的自由度，提升计算效率。

1. 材料

“模态分析”需要定义的材料有：

坝体材料：

• “混凝土密度”($kg/m^3$)
• “弹性模型”($GPa$)
• “泊松比”

坝基材料：

• “弹性模量”($GPa$)
• “泊松比”

“模态分析”依赖于结构的质量和刚度分布，质量和刚度分布由“密度”、“弹性模量”和“泊松比”等材料属性决定。用户可根据实际需要更改材料参数。

2. 载荷

“模态分析”需输入的载荷为：

• “上游水位”（$m$）

重力坝在运行期上游面与水接触，混凝土结构与水的相互作用很大程度上影响重力坝的振动特性。用户可根据水库设计水位定义上游水位载荷。

3. 仿真模型

在模态分析中，混凝土结构与水的相互作用以动水作用对坝体产生的压力形式体现。软件提供两种地震动水压算法：

• “附加质量”
• “可压缩库水模型”

“附加质量”是一种拟静力分析方式，其原理是把动水的效应等效为重力坝坝体上游的压力分布。软件采用 Westergaard 方法定义压强分布： $$p\left(y\right)=\frac{7}{8}k\gamma_w(hy)^\frac{1}{2} \tag{4}$$ 其中:

• $p\left(y\right)$为水深$y$处的压强（$Pa$）
• $k$为拟静力系数，即水平地震加速度系数与重力加速度的比值
• $\gamma_w$为水的容重(N/m3)
• $h$为上游水深($m$)

软件根据用户定义的上游水位会自动计算出坝体上游面动水压分布。

“可压缩库水模型”体现了在动力学持续作用下水体随大坝做往复运动的效应，即以波动方程的形式考虑上游库水的动水压力场。

当选择“可压缩库水模型”时，用户需额外定义的参数有：

• 水的密度 $\rho_w$($kg/m^3$)
• 水中声速 $c_w$ ($m/s$)

可压缩库水模型在流体域考虑无粘流体可压缩性，求解以浮动压力 $p$为未知量的 Helmholtz 方程：

$$ \Delta p + \frac{\omega ^2 }{c_w^2}p = 0 \tag{5} $$

在固体域求解弹性力学平衡方程，流固耦合面满足受力平衡和运动兼容条件：

流体单元模型在模拟作用于上游面动水压力的同时产生声波形式的能量耗散，因此低阶固有频率略低于附加质量法计算结果。

4. 计算结果

点击左边栏下方的“开始计算”按钮，软件会根据用户的参数设置进行模态分析。

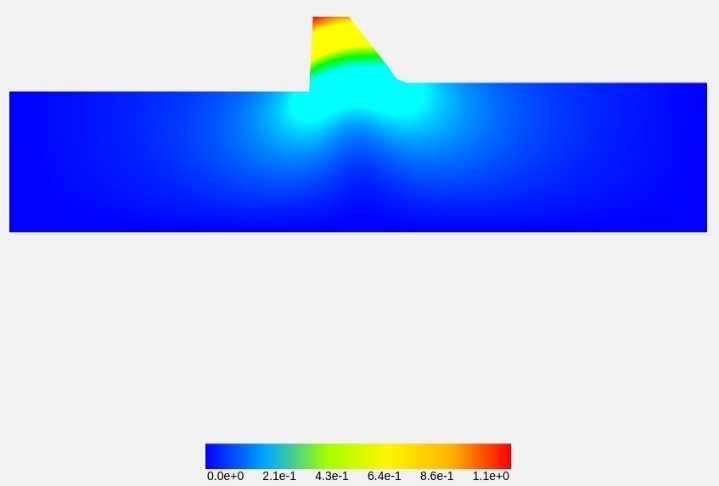
计算成功后会显示“计算成功”标签。此时页面的中部会出现重力坝坝体和坝基的模态振型结果云图。云图中的物理场为位移，单位为($m$/s)，数值对应下方刻度条。

在页面右侧可点击“计算结果”展开模态振型结果表格。

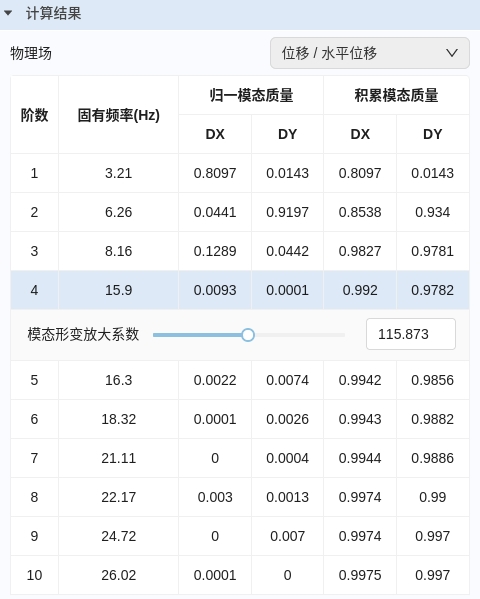
其中，通过切换“物理场”选项卡可以显示不同物理量的表格结果：

• “位移/水平位移”
• “位移/垂直位移”
• “总位移”

与此同时，页面中部的模态云图结果也会随之切换为对应的物理场结果。

表格结果中的“阶数”代表结构的模态振型阶数，展示前 10 阶模态，按照固有频率从小到大排序。每一阶模态的结果包括：

• “归一模态质量”
• “累积模态质量”

每种结果包含“水平”和“竖直”两个方向的分量，“DX”表示水平方向，“DY”表示竖直方向。

“归一模态质量”表示该阶模态对动态激励的参与程度，“累积模态质量”是对前面“归一模态质量”的求和，有助于分析考虑的模态阶数是否足够。

通过点击不同“模态阶数”所在的行，页面中部的云图会对应切换到该阶模态的振型，该行下方会弹出“模态形变放大系数”，通过拖动进度条或者输入数值的方式，可以改变云图中位移场的放大程度，以便观察模态振型结果。

静力/拟静力分析

静力/拟静力分析提供“有限元法”和“材料力学法”两种计算方法，支持热固耦合分析和9种力学载荷定义与载荷组合，计算大坝应力状态、坝基面抗滑稳定性和深层抗滑稳定性，根据水利、电力行业规范和CFBR法国大坝水库委员会标准规范进行结构安全评价。

当“求解方法”为“有限元法”时，通过切换“采用热固耦合”下拉菜单中的选项卡，可以选择是否在“静力/拟静力分析”中应用“传热分析”的温度场结果。在用户已经进行过“传热分析”后，才能选择“是”。

1. 材料

重力坝计算的材料参数分“坝体材料参数”、“坝基材料参数”和“通用材料参数”，具体包括： 坝体材料参数：

• “密度”（$kg/m^3$）
• “弹性模量”（$GPa$）
• “泊松比”
• “热胀系数”（$K^{-1}$）
• “参考温度”（$\degree C$）

坝体材料参数：

• “弹性模量”（$GPa$）
• “泊松比”

通用材料参数：

• “摩擦系数”
• “凝聚力”（$MPa$）

其中，“热胀系数”和“参考温度”是热-力耦合计算参数，仅在使用“有限元法”计算下且“采用热固耦合”为“是”时出现。

“摩擦系数”和“凝聚力”是计算抗滑稳定计算和抗剪强度计算用到的材料参数，通过输入这些参数，软件会自动计算并评价结果是否符合规范要求。

2. 载荷

根据《混凝土重力坝设计规范》，重力坝载荷的“基本组合”包括：

• 1）“正常蓄水位工况”
• 2）“设计洪水位工况”
• 3）“冰冻工况。”

“特殊组合”包括：

• 1）“校核洪水位工况”
• 2）“地震工况”

软件中预先定义了规范中要求的载荷组合形式，下拉“载荷组合”并选择以上提到的组合类型即可快速选中“基本组合”或“特殊组合”。

软件同样支持用户“自定义组合”方式，如命名“自定义组合名称”为“自定义组合 1”，勾选“永久设备自重”、“静水压力”、“扬压力”、“浪压力”和“地震”。

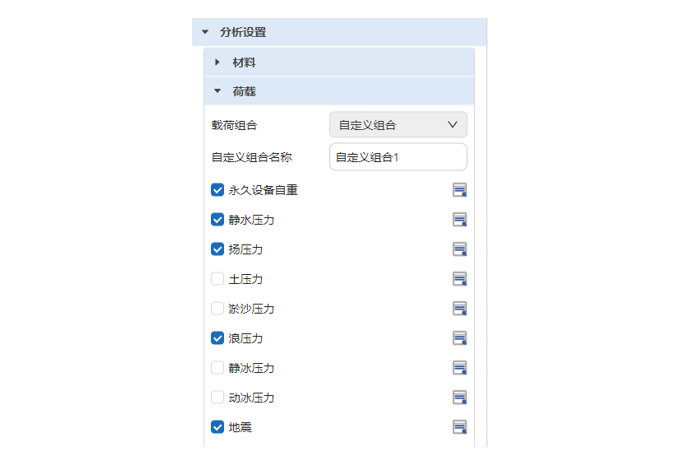
软件的载荷选项参照《水工建筑物载荷标准》设置，总计 9 种类型:

• “永久设备自重”
• “静水压力”
• “扬压力”
• “土压力”
• “淤沙压力”
• “浪压力”
• “静冰压力”
• “动冰压力”
• “地震”

提示：

载荷组合设置功能支持历史计算结果的记录，在“计算结果”窗口中用户可切换相同大坝几何和网格情况下已提交计算的载荷组合，实现计算结果的切换查看，便于不同大坝运行工况的结构安全评价结果对比分析。

2.1 永久设备自重

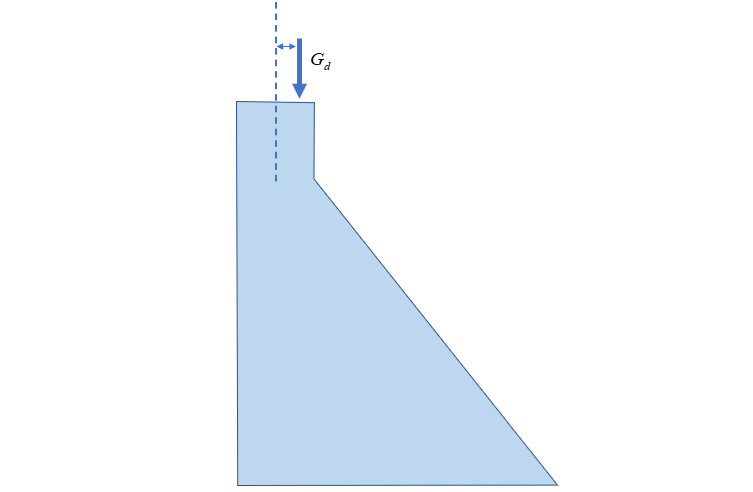
“永久设备自重”为重力坝坝顶的厂房设备等的重力载荷，需输入的参数为：

• “设备重量”（$kN$）
• “设备位置”

“设备重量”为坝顶设备的总重力。“设备位置”为设备的重心相对于坝顶中轴线的偏移程度，可输入-1 到 1 之间任意浮点数，上游为负，下游为正，0 值表示设备恰好位于坝顶中心位置；

2.2 静水压力

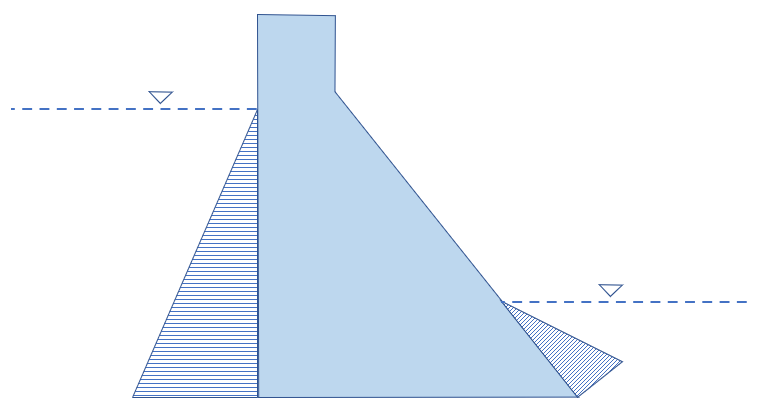
“静水压力”为上游、下游的水压力，需输入的参数为：

• “上游水位” $H_{am}$（$m$）
• “上游水位” $H_{av}$（$m$）

“静水压力”根据输入的“上游水位”和“上游水位”自动计算：

$$ P_w(y)=\rho_w g\left(H_{am/av}-y\right) \tag{7} $$

在勾选“采用热固耦合”时，需检查静水压力中的水位设置是否与传热分析中的设置一致。

2.3 扬压力

“扬压力”是上下游水位产生的渗流作用与坝基面的力，属于一种不利载荷，分为托浮力和渗透压力，其中托浮力是由下游水位产生的浮力，渗透压力是上游水位高于下游部分所产生的渗流压力。

“中国标准（GB）”中有两种定义方式：

• 仅勾选“防渗帷幕和排水孔”
• 同时勾选“防渗帷幕和排水孔”和“坝基抽排系统”

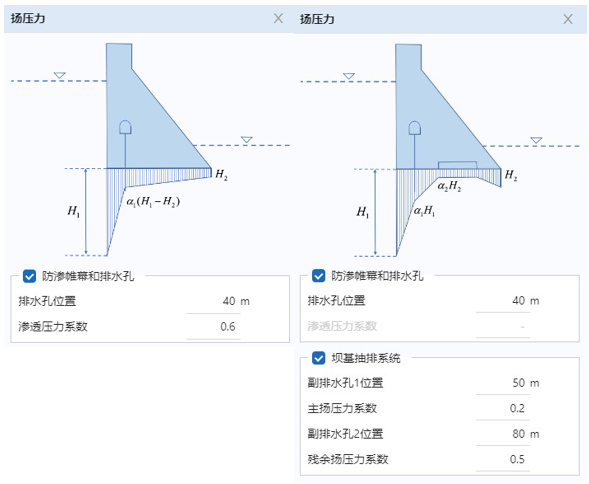
仅勾选“防渗帷幕和排水孔”时，需输入的参数为：

• “排水孔位置”($m$)
• “渗透压力系数” $\alpha$

此时，坝基的扬压力以双线性形式定义，通过选择“排水孔位置”和“渗透压力系数”分别定义扬压力折减的位置（防渗帷幕位置）以及折减系数。

在“防渗帷幕和排水孔”排水设计方案基础上可增加“坝基抽排系统”，需输入的参数为：

• “防渗帷幕和排水孔”参数：

  • “排水孔位置”（$m$）

• “坝基抽排系统”参数：

  • “副排水孔位置 1”（$m$）
  • “主扬压力系数” $\alpha_1$
  • “副排水孔位置 2”（$m$）
  • “残余扬压力系数” $\alpha_2$

注意：

当采用“坝基抽排系统”排水设计时，坝基扬压力分布用多段线性函数定义，主排水孔之前定义为扬压力，主排水孔之后定义为残余扬压力，当用户选择“电力行业规范”时，需分别定义扬压力和残余扬压力分项系数，而不做托浮力和渗透压力的区分。

计算选用的扬压力系数建议值可参照下表：

2.4 土压力

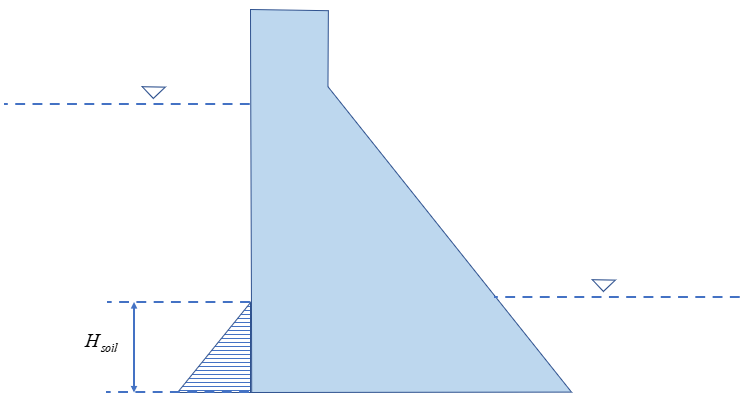
“土压力”为坝体上游存在填土时，重力坝相对于土体的位移状况受到的土压力作用,需要输入的参数有：

• “土浮容重” $\gamma_s$（ $kN/m^{3}$）
• “土层厚度” $H_s$（ $m$ ）
• “静止土压力系数” $K_0$

软件根据输入的“土浮容重”、“土层厚度”和“静止土压力系数”（范围从 0 到 1）计算得到“土压力”随高程的分布。水平方向土压力计算式为：

$$ P_{soil, h}(y) = (\gamma_s (H_{soil} - y) + p_{sed})K_0 \tag{8} $$

其中 $p_{sed} = \gamma_{sed}H_{sed}$ 表示淤沙对土压力的附加作用。

当坝体上游面存在向下游倾斜的倾角时，土压力存在竖向分量。软件自动计算坝体与土层上表面交点 $x_1$关于坝踵 $x_0$的相对水平距离 $\Delta x$，当 $\Delta x = x_1 - x_0 > 0$时，将土层高程范围坝体上游面几何按线性分布近似处理，土压力竖向分量计算为：

$$ P_{soil, v}(y)=-\gamma_{s} \frac{\Delta x}{H_{soil}}\left(H_{soil}-y\right) - p_{sed} \tag{9} $$

静止土压力系数 $K_0$的建议值可参照下表。

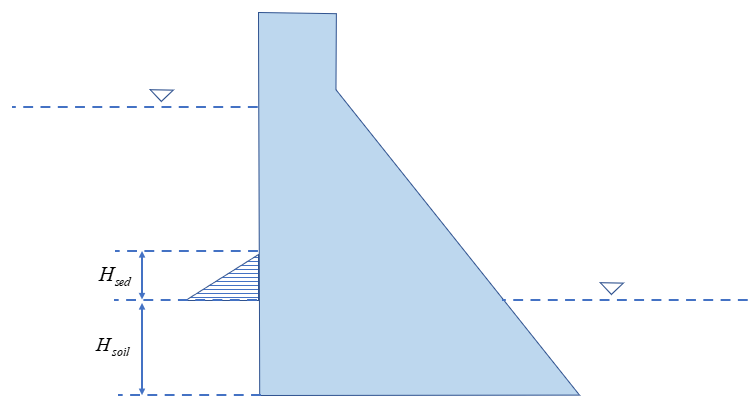
2.5 淤沙压力

“淤沙压力”考虑上游水库泥沙冲淤的效应，其计算根据朗肯理论主动土压力公式。需要输入的参数有：

• “淤沙浮容重” $\gamma_{sb}$（ $kN/m^3$ ）
• “淤积厚度” $H_{sed}$（ $m$ ）
• “淤沙内摩擦角” $\phi_s$ （°）

其中淤沙浮容重可通过淤沙干容重 $\gamma_{sd}$ 和孔隙率 $n$ 计算：

$$ \gamma_{sb}=\gamma_{sd}-(1-n) \gamma_w \tag{10} $$

与土压力相似，淤沙压力分为水平力和竖向力，后者仅当淤沙范围内坝体上游面存在向下游的倾角时存在，分别计算为：

2.6 浪压力

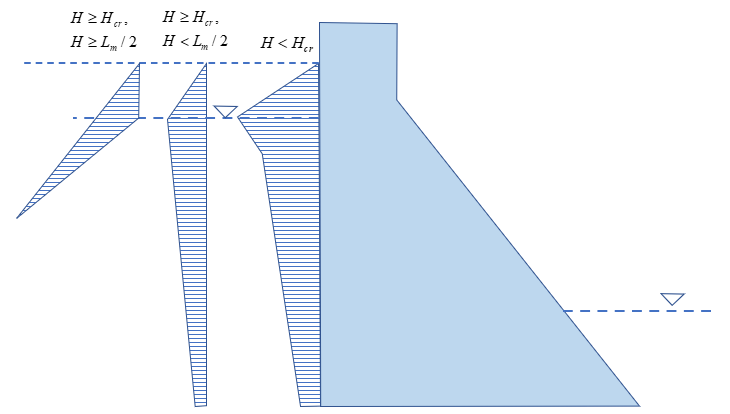
“浪压力”考虑由风浪产生的浪压力的效应。目前的波浪要素的计算均采用以一定实测或试验资料为基础的半理论半经验性方法。软件提供三种基于观测资料的回归分析模型来计算波浪要素：

• “莆田试验站公式”
• “鹤地水库公式”
• “官厅水库公式”

其中，“莆田试验站公式”比较适用于我国东南沿海及内陆平原水库的浅水波浪计算，需输入的参数有：

• “风区长度”（$km$）
• “计算风速”（$m/s$）
• “平均水深”（$m$）

“鹤地水库公式”和“官厅水库公式”比较适合于深水波浪计算，需输入的参数有：

• “风区长度”（$km$）：鹤地水库公式需<7.5 $km$，官厅水库公式需<20 $km$。
• “计算风速”（$m/s$）：鹤地水库公式需<26.5 $m/s$，官厅水库公式需<20 $m/s$。

2.7 静冰压力

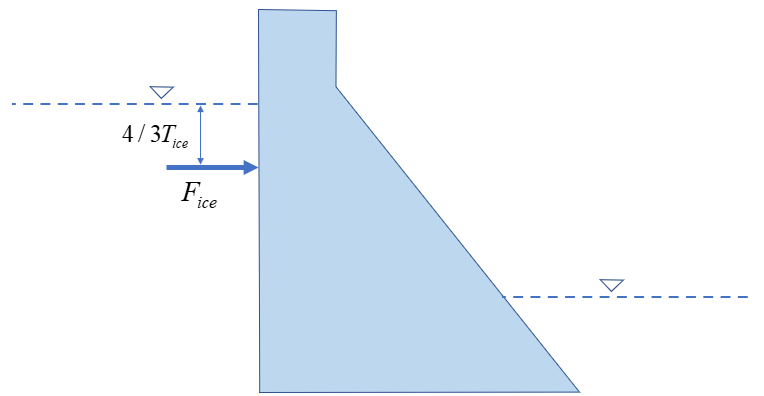
“静冰压力”考虑在冬季水库表面结冰时，冰对坝体上游表面的挤压作用，其分布视作沿冰厚分布的上大下小的倒三角形，其作用点在冰面以下距冰面 1/3 冰厚处。需要输入的参数为：

• “冰层厚度”（$m$）

静冰压力根据冰层厚度按下表通过线性插值计算标准值：

2.8 动冰压力

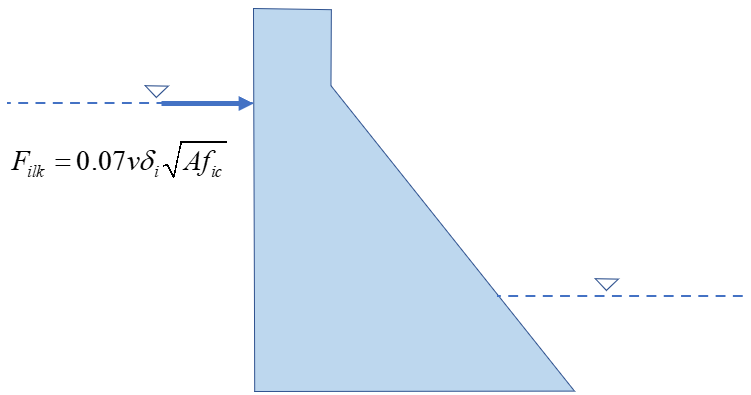
“动冰压力”考虑上游面受到运动的冰块撞击的效应，当冰块垂直或接近垂直撞击坝面时，“动冰压力”的计算公式为：

$$F_{ilk}=0.07V_id_i\sqrt{A_if_{ic}} \tag{12}$$

其中，需要输入的参数为:

• “冰块运动速度” $V_i$（$m/s$）
• “流冰厚度” $d_i$（$m$）
• “冰块面积” $A_i$（$m^2$）
• “冰的抗压强度” $f_{ic}$（$MPa$）

2.9 地震

“地震载荷”按拟静力法计算。需要输入的参数为:

• “水平峰值地震加速度” $a_h$（$m/s^2$）
• “竖直峰值地震加速度” $a_v$（$m/s^2$）
• “水平地震系数” $\alpha_h$
• “竖直地震系数” $\alpha_v$

欧标与国标地震载荷计算方法不同：

欧洲标准（CFBR）:

“地震系数”为欧标概念，仅“欧洲标准（CFBR）”情况下需要输入，建议取值 $\alpha_h = 2/3$, $\alpha_v = 0.2$，地震惯性力以体积力形式加载，计算式为：

地震动水压力采用 Westergaard 公式（4）计算。

中国标准（GB）:

根据 NB 35047-2015《水电工程水工建筑物抗震设计规范》软件自动计算地震惯性力动态分布系数：

$$ \alpha(y) = 1.4 \frac{1 + 4 (y / H)^4} {1 + 4 \int_S \frac{\rho g}{G_{dam}}(y/H)^4dS} \tag{14} $$

注意：

为确保有限元法和材料力学法计算结果一致性，两种方法均基于网格模型，采用同样的数值积分公式计算地震惯性力动态分布系数，材料力学中“计算质点”即“网格单元节点”，等效地表示坝体的空间数值离散。

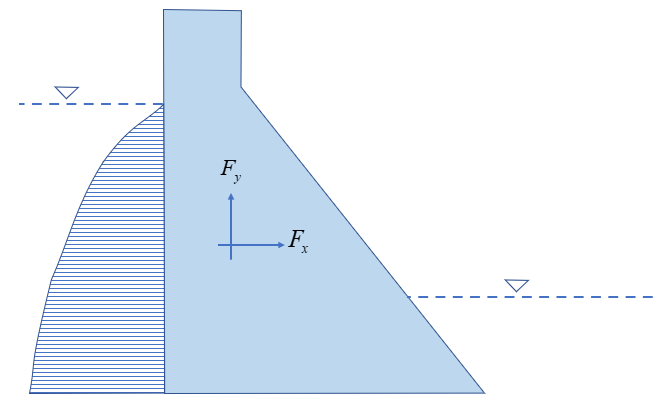
地震惯性力仅考虑水平分量，计算式为：

$$ E_{ih}(y) = 0.25a_h \rho \alpha(y) \tag{15} $$

地震动水压力计算式为：

$$ P_{dyna}(y) = 0.25a_h\psi(H_{am} - y)\rho_w H_{am} \tag{16} $$

其中动水压力分布系数 $\psi(h)$是关于水深 $h$的函数。

3. 评价指标

当且仅当用户选择“电力行业规范”时，可在“评价指标”选项卡中设置材料性能和载荷作用分项系数等可靠度计算相关参数。

“材料性能系数”包括：

• “结构重要性系数” $\gamma_0$

  对于结构安全级别分别为 I、II、III 的重力坝分别取值为 1.1、1.05 和 1.0。

• “设计状况系数” $\psi$

  根据工况类型选取，持久设计状况、短暂设计状况和偶然设计状况分别取值 1.0、0.95he 0.85。

• “基岩/混凝土抗压强度” $f_{ck}$（$MPa$）

  根据大坝混凝土强度等级，可参照下表选取：

“作用系数”包括：

• “材料性能系数”

  需设置坝基面、深层滑动面（结构面）上摩擦系数和凝聚力分项系数，以及混凝土抗压强度材料分项系数 $\gamma_m$。

• “作用系数”

  需设置自重和其他 9 种力学载荷的作用系数，其中扬压力载荷按排水方案不同需区分渗透压力、托浮力、主扬压力和残余扬压力分项系数。动冰压力和静冰压力采用相同分项系数。

4. 计算

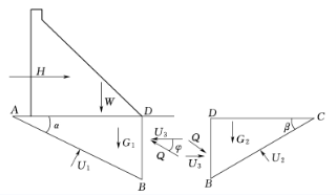
在“计算”设置中，可以通过勾选或不选“深层抗滑稳定”来决定是否进行“重力坝深层抗滑稳定”计算。软件支持双滑动面的抗滑稳定计算，以应对坝基深层存在缓倾角软弱结构面的情况。

通过定义如图所示的“滑动块 ABD”和“滑动块 BCD”的几何坐标和材料参数，考虑主滑动体 ABD 与辅助滑动体 BCD 具有同等安全度，可以计算得到滑动体的“抗滑稳定安全系数”。

此时，需要输入的参数有：

“滑动面定义”参数：

• “A 点 X 坐标” $x_B$（$m$）

• “C 点 X 坐标” $x_C$（$m$）

• “B 点 X 坐标” $x_A$（$m$）

• “中间破裂面深度”（$m$）

• “中间破裂面抗力夹角” $\phi$（$m$）

  仅“材料力学法”需输入。

“滑动体密度”参数：

• “主滑动体密度”（$kg/m^3$）
• “辅助滑动体密度”（$kg/m^3$）

“滑动面抗剪强度”参数：

• “主滑动面（AB）凝聚力” $c_1$（$MPa$）
• “辅助滑动面（BC）摩擦系数” $f_1$
• “主滑动面（AB）凝聚力” $c_2$（$MPa$）
• “辅助滑动面（BC）摩擦系数” $f_2$

在“求解方法”选择为“有限元法”时，深层抗滑稳定的分析方法为“应力代数和比值法”，否则软件采用刚体极限平衡法中的“等安全系数法”计算。此时用于有限元计算的网格会更新，根据输入在滑动面周边进行加密，以计算深层抗滑稳定系数。

“应力代数和比值法”根据有限元计算结果，提取滑动面上法向和切向应力，通过积分计算抗滑稳定安全系数：

$$ K_s = \frac{\sum_{i=1}^{n}(f_i \sigma_{n,i}+c_i)l_i}{\sum_{i=1}^n\tau_{n,i}l_i} \tag{17} $$

“等安全系数法”分别计算主滑动面 AB 和辅助滑动面 BC 的抗力函数 $R(\cdot)$和作用函数 $S(\cdot)$，对于主滑动面 AB：

$$ S_1(\cdot) = \left(\sum W + G_1\right)sin\alpha + \sum P cos\alpha - Q cos(\phi - \alpha) - U_3cos\alpha \tag{19} $$

对于辅助滑动面 BC：

$$ \begin{aligned} R_2(\cdot) = f_2\left[G_2cos\beta + Q sin(\phi + \beta) + U_3 sin\beta - U_2 \right] + c_2 A_2 \end{aligned} \tag{20} $$

$$ S_2(\cdot) = Q cos(\phi + \beta) - G_2 sin\beta + U_3cos\beta \tag{21} $$

其中 $\sum W$为载荷垂向力之和，$\sum P$为作用于滑动面载荷水平向力之和，$U_1$、$U_2$和 $U_3$分别表示主滑动面、辅助滑动面和中间破裂面扬压力，$Q$表示接触面 BD 上的抗力，为待求解未知量。

考虑到一般情况下主滑动面与辅助滑动面没有完全贯通，存在阻水效应，故采用随深度渐减型扬压力计算式：

5. 计算结果

计算完成后，点击展开页面右侧的“计算结果”可以查看计算的表格结果。

“载荷组合”对应“分析设置”中定义的载荷组合名称，用户可切换查看历史计算结果。

“物理场”仅在“有限元法”下出现，“物理场”包含三类物理量，每种“物理场”有不同方向的分量，具体为：

• “位移”：分为水平、垂直和总位移。
• “应力”：分为 X 和 Y 法向应力
• “等效应力”：分为第一（最大）和第二（最小）主应力。

“建筑物级别”选项仅适用于“水利行业规范”，表示所分析的重力坝水工建筑物级别，有“1”、“2”、“3”三个等级，级别具体划分规则参照 SL252-2017《水利水电工程等级划分及洪水标准》相关规定。软件根据用户选定的安全级别自动调整对应的安全“阈值”，进行抗滑稳定安全评价。

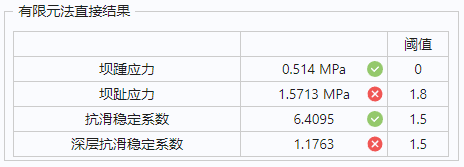
“有限元法直接结果”表格为“有限元法”计算结果，对应的是规范中要求校核的量，包括：

• “坝踵应力”（$MPa$）

  坝踵线性化应力，压应力为正，拉应力为负，计算式为：

  $$ S_{am} = \frac{\sum W_R}{A_R} + \frac{\sum M_R T_R}{J_R} \tag{23} $$

  其中 $N = \sum W_R$表示坝基面法向作用力之和，$M = \sum M_R$表示关于坝基面形心力矩之和，$T_R$为坝踵或坝趾到形心轴的距离，$J_R$为坝基面对形心惯性矩。

• “坝趾应力”（$MPa$）

  坝趾线性化应力，压应力为正，拉应力为负，计算式为：

  $$ S_{av} = \frac{\sum W_R}{A_R} - \frac{\sum M_R T_R}{J_R} \tag{24} $$

• “抗滑稳定系数”

  根据抗剪断强度公式计算的坝基面抗滑稳定性系数。

• “深层抗滑稳定系数”（仅勾选“深层抗滑稳定”时）

  根据“应力代数和比值法”或“等安全系数法”计算的深层抗滑稳定性系数。

若表格第二列的计算结果后方出现“对勾”则说明符合规范要求，若计算结果后方出现“红叉”则说明计算结果超出规范允许的范围。

“坝踵应力”根据《混凝土重力坝设计规范》不应出现拉应力，即阈值为 0。在勾选“水利行业规范”时，“坝趾应力”不应大于坝体混凝土容许压应力，并不应大于基岩容许承载力，其阈值需根据实际工程情况判定。“抗滑稳定系数”根据“抗剪断强度公式”计算，大于阈值说明坝体整体稳定性符合规范要求；“深层抗滑稳定系数”在勾选“深层抗滑稳定”后计算，大于阈值说明“深层抗滑稳定”符合规范要求。

在使用“电力行业规范”进行安全校核时，相应的计算结果展示结构可靠度（安全裕度）系数，校核大坝抗压、抗拉和抗滑稳定极限承载能力。

“静力/拟静力中间结果”是“有限元法”或“材料力学法”计算规范要求评估的物理量的过程中出现的中间结果，均以支反力或支反力矩的形式表示，包含：

• “法向力” $N = \sum W_R$（$kN$）

  作用于坝体上全部载荷（不包括扬压力）在坝基面上产生的支反力法向分量。

• “切向力” $T = \sum P_R$（$kN$）

  作用于坝体上全部载荷（不包括扬压力）在坝基面上产生的支反力切向分量。

• “扬压力”（$kN$）

  坝基面承受的扬压力

• “总力矩” $M = - \sum M_R$（$kN$.m）

  坝基面上关于形心的支反力合力矩

• “薄膜应力” $\sigma_m = N/A_R$（$MPa$）

• “弯曲应力” $\sigma_b = - M T_R/ J_R$（$MPa$）

当勾选“深层抗滑稳定计算”时，结果栏下方会显示“深层抗滑稳定中间结果”表格。

“有限元法”使用“应力代数和比值法”计算了“主滑动面”和“辅助滑动面”的结果，包含：

• “抗滑力”（$kN$）
• “滑动力”（$kN$）

“静力/拟静力法”使用“等安全系数法”，除“有限元法”包含的计算结果以外，还包含： “主滑动面”和“辅助滑动面”：

• “扬压力”（$kN$）

“中间滑动面”：

• “抗力”（$kN$）
• “扬压力”（$kN$）

时程分析

“时程分析”分析类型仅在求解方法选择“有限元法”时出现，该分析类型能够综合考虑“传热分析”、“模态分析”和“静力/拟静力分析”的影响，用于分析重力坝在地震作用下的动力学响应。

与“有限元法”的“静力/拟静力分析”相同，通过“采用热固耦合”选项可以选择是否考虑坝体的温度效应。

1. 材料

“材料”选项中定义时程分析的通用材料参数，包括：

“坝体材料参数”：

• “密度”（$kg/m^3$）
• “弹性模量”（$GPa$）
• “泊松比”
• “热胀系数”（$K^{-1}$）
• “参考温度”（$\degree C$）

“坝基材料参数”：

• “弹性模量”（$GPa$）
• “泊松比”

“通用材料参数”：

• “摩擦系数”
• “凝聚力”（$MPa$）
• “阻尼”

“热胀系数”和“参考温度”仅当选择“采用热固耦合”时出现。

软件提供两种“阻尼”模型：

“模态阻尼”需为各土层设置：

• “振型阻尼比”

  常值模态阻尼比，定义为：

  $$ \xi=\frac{\eta}{2}=\frac{E_{d, cycle}}{4 \pi E_{p, max}} \tag{21} $$

其中为 $\eta$ 损失系数，表示一个振动周期耗散能与 $2\pi$ 倍最大变形势能的比值。例如，振型阻尼比取值 0.02，表示每个振动周期发生 2%的振幅衰减。

瑞利阻尼需为坝体和坝基分别设置阻尼模型参数：

• “$\alpha$”（$s^{-1}$）
• “$\beta$”（$s$）

动力学方程中阻尼矩阵计算为：

$$ \mathbf{C}=\alpha \mathbf{M}+\beta \mathbf{K} \tag{22} $$

2. 载荷

“载荷”设置中有四个输入项：

• “重力加速度” $g$ （$m/s^2$）
• “静水压力”
• “扬压力”
• “加速度谱”

“静水压力”与“扬压力”与“静力/拟静力分析”中定义方式相同。

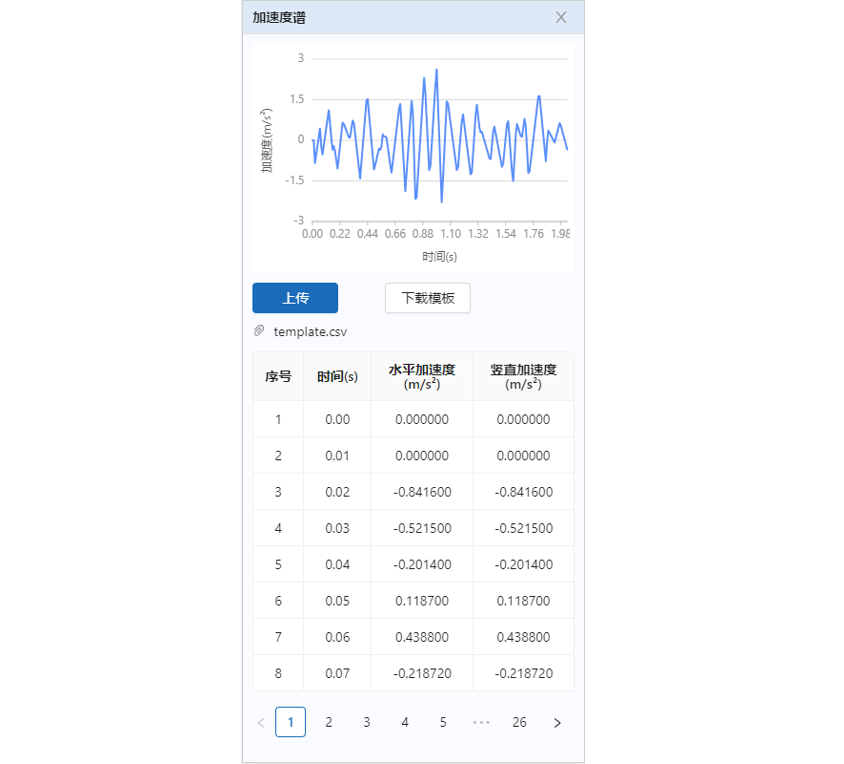
点击“加速度谱”的编辑图标弹出参数输入窗口，窗口上方是“加速度谱”的预览折线图，下方表格中显示具体数值。曲线的自变量为时间（$s$），后两列分别为“水平加速度”（$m/s^2$）和“竖直加速度”（$m/s^2$）,用户可以点击“下载模板”下载加速度谱的模板文件（template.csv），根据自己的需要修改“加速度谱”并通过“上传”按钮重新导入新的“加速度谱”用于计算。

3. 仿真模型

软件提供两种“地震动水压算法”:

• “附加质量”
• “可压缩库水模型”

和两种“坝基地震动输入算法”:

• “无质量地基模型”
• “平面波模型”

可任意组合分析，即总计 4 种仿真模型。

“附加质量”和“可压缩库水模型”，是“时程分析”中不同的考虑库水作用的方式。“附加质量”是一种拟静力模型，通过在坝体上游表面的单元上设置额外的质量模拟库水的压力效应；“可压缩库水模型”是一种流固耦合算法，选择“可压缩库水模型”后，软件会自动生成加入库水的网格用于计算，其考虑了库水的压缩性以及压力场的动态变化过程，需额外输入的参数为：

• “水的密度”（$kg/m^3$）
• “水中声速”（$m/s$）

“无质量地基模型”和“平面波模型”，是“时程分析”中不同的考虑地震载荷激励的方式。“无质量地基模型”复用“模态分析”的结果，在模态空间下施加“水平”和“竖直”方向的地震激励，计算各阶模态振型结果；“平面波模型”是一种等效地震动载荷输入方式，需额外输入的参数为：

• “坝基密度”（$kg/m^3$）。

4. 后处理

软件提供在“后处理”中提供查看任意点结果曲线的功能。展开后处理”选项卡，默认提供两个兴趣点。

激活“鼠标拾取”模式，单击页面中部的重力坝模型可以拾取点的“X 坐标”和“Y 坐标”，并将其添加至兴趣点列表；此外，激活“手动编辑”模式，通过“添加兴趣点”也能够“新建兴趣点”。在表格中，可根据需要修改 X 坐标和 Y 坐标。勾选表格中相应兴趣点前的方框，通过“删除兴趣点”按钮可以删去多余的兴趣点。

5. 计算结果

计算完成后，展开页面右侧的“计算结果”选项卡，可以查看时程分析计算结果。

计算结果中的“物理场”选项卡用于切换页面中部的云图结果。云图结果展示的是计算时间范围内不同“物理场”的最大值和最小值，根据“物理场”选项卡旁的“最大”和“最小”切换。“物理场”结果包含：

• “加速度”：包括水平、垂直和总加速度（$m/s^2$）。
• “速度”：包括水平、垂直和总速度（$m/s$）。
• “位移”：包括水平、垂直和总位移（$m$）。
• “应力”：包括 X 和 Y 方向法相应力（$Pa$）。
• “主应力”：包括第一（最大）和第二（最小）主应力（$Pa$）。

下方展示“兴趣点”的时程响应结果。切换兴趣点，可以查看不同兴趣点的结果。下拉“曲线图”选项卡，可以切换“位移”、“速度”、“加速度”和“应力和稳定性”物理量的变化曲线。物理量各个分量的曲线图会同时展示，曲线的横坐标为“时间”，纵坐标为物理量的“计算结果”。