分析设置

土石坝软件提供渗流仿真分析、整体稳定分析和动力学时程分析三种仿真计算，满足土石坝设计和工程安全校核需求。用户可在“分析类型”选项中切换。

渗流仿真分析

渗流仿真分析通过求解非饱和-非稳定渗流方程计算大坝孔隙压力场，进而计算渗流速率、单宽渗流量和渗透比降等渗透稳定关键评价指标，为土石坝等土工结构材料选取、防渗系统设计和工程预测性运维提供参考依据。其中土体渗流规律由达西定律描述，水分特征由Mualem-Van Genuchten模型描述。非饱和瞬态渗流控制方程为：

$$\{\begin{array}{l}{\dot{m}}_w+\nabla \cdot {\mathbf{F}}_w=0\\ {\dot{m}}_g+\nabla \cdot {\mathbf{F}}_g=0\end{array}\text{\hspace{1em}(1)}$$

其中 $m$ 和 $\mathbf{F}$ 分别表示气相或液相容重和质量流量。

用户可通过“计算类型”选项选择稳态或瞬态渗流计算。瞬态渗流用于模拟水位骤降或周期性变化时渗流孔隙压力场瞬态变化过程，例如在库水位降落时结合整体稳定分析功能评估上游坝坡边坡稳定性。

对于瞬态渗流计算，用户仅需输入水位变化过程函数（通过表格或公式定义），同时激活“自动延长时间步至稳态”选项，软件自动计算从水位变化最后时刻到大坝渗流孔隙压力场稳定的全过程。

1. 材料

在水力学材料参数输入窗口中，用户需定义水的基本物理性质和大坝各区域水力学参数：

• “水的密度” ${\rho }_w$ $(kg/m^3)$
• “水动力学粘度” $\mu$ $(Pa.s)$
• “比奥系数” $b$

其中水动力学粘度和比奥系数在V1.0软件中对计算结果没有影响，可保留其默认值 $\mu =10^{-3}Pa.s$，$b=1.0$。

对于大坝各区域，水力学材料参数包括：

• “水平和垂直渗透系数” $k_L$、$k_N$（m/day）
• “孔隙率” $\varphi$
• “VG模型参数” $Pr$（MPa）、$N$

其中渗透系数和孔隙率用于计算渗流控制方程(1)中容重和质量流量：

$$m_p={\rho }_p\varphi S_p-{\rho }_p^0{\varphi }^0{S}_p^0\text{\hspace{1em}(2)}$$

$${\mathbf{F}}_p=-{\rho }_p\varphi S_{p}k\vec{\nabla }H\text{\hspace{1em}(3)}$$

$H$表示相应位置的水头。

Van Genuchten模型描述土体有效含水量 $S_{we}$ 与孔隙压力 $P_c$ 的关系，一般可根据土体持水曲线或土颗粒级配曲线拟合得到：

$$S_{we}=\frac{S_w-S_r}{1-S_r}={\left[1+{\left(\frac{P_c}{P_r}\right)}^N\right]}^{-m}\text{\hspace{1em}(4)}$$

其中 $S_r$ 表示滞留含水率，本软件取值 $S_r=0$，$m=1-1/N$ 为常数。

渗透系数和孔隙率可根据表 1（GB50286-98《提防工程设计规范》）选取。

2. 边界

渗流计算中，用户需设置上下游水头边界条件。输入参数包括：

• “库水位” $H_{am}(t)$
• “下游水位” $H_{av}(t)$

边界水头根据用户输入的库水位和下游水位随时间（天）变化关系自动计算。稳态计算时，库水位和下游水位为常数，瞬态计算时 $H_{am}(t)$、$H_{av}(t)$ 可通过“表格”或“公式”两种方式输入。

表格输入时，用户需给出不同时刻（天）对应的库水位或下游水位（$m$）列表，软件自动通过插值方法计算任意时刻的函数值。在“高级设置”选项中，可选择函数左右端“延拓方式”，包括：

• “常数”：左右端以外函数值恒等于插值列表第一个/最后一个值。
• “线性”：左右端以外函数值根据插值列表前两个/后两个值按线性规律延拓计算。

同时用户可选择插值列表中计算函数值的插值方法，包括“指数”或“线性”。

公式输入时，用户可使用公式编辑器键入公式，其中时间（天）变量名称规定为“DAY”。例如水位在4天内在0m至60m之间按正弦规律变化，水位变化公式可写为30 * (1 – sin(2 * pi / 4 * DAY))。

3. 时间步

在“时间步”选项卡中，用户可设置计算时间步并控制结果写入时间步。计算时间步规定从第0天开始，有两种设置方式：

• 均匀时间步

  • “仿真时间”：渗流仿真总时长（天）。
  • “步数”：划分时间间隔总数。

• 非均匀时间步

  用户通过表格方式设置时间列表和时间步数量列表。例如时间列表为[1, 2, 4], 时间步数量列表为[1, 1, 2]，则表明计算时间步列表为[0, 1, 2, 3, 4]。

为了防止计算时间步设置过于密集导致后处理计算效率降低，用户可将“写入时间步”选项由“按计算时间步写入”改为“等间隔步数写入”，同时定义“写入间隔步数”，表示写入计算结果进行后处理的时间步列表重采样间隔。

4. 计算结果

稳态渗流计算结果包括：

• “水头”：总水头和压力水头，可选择云图或等值线展示方式。
• “渗流速率”：水平和垂直方向渗流速率，以及总渗流速率，可选择云图或箭头展示方式。
• “渗透比降”：可选择云图展示方式。

此外，软件以表格形式给出大坝单宽渗流量、最大渗透比降及其位置坐标。

瞬态渗流计算支持将上述结果以云图、等值线、箭头形式按时间步播放展示，同时绘制单宽渗流量和渗透比降随时间变化曲线。

整体稳定分析

整体稳定分析功能用于评估大坝上下游边坡在多种静力载荷、地震惯性力和孔隙水压力作用下的滑动失稳风险，提供圆弧、非圆弧极限平衡法（Limit Equilibrium Method, LEM）和有限元强度折减法（Strength Reduction Method, SRM）等多种稳定性系数（Factor of Safety, FS）计算方式。模块同时支持地震屈服加速度和危险滑动体的分析计算，作为基于动力学时程分析计算边坡地震永久变形的前置计算。

用户可在“整体稳定分析方法”选项中选择以下计算方法：

• “瑞典圆弧法”

  基于圆弧滑动面假设的刚体极限平衡法，忽略条间力和竖向力，仅考虑滑动体整体力矩平衡，计算速度快，但结果偏保守，不推荐使用。

• “简化毕肖普法”

  基于圆弧滑动面假设的刚体极限平衡法，假设条间力为水平力，满足土条竖向力和整体力矩平衡，适用于均质坝、厚斜墙或厚心墙坝。

• “摩根斯坦-普莱斯法”

  基于非圆弧滑动面假设的刚体极限平衡法，完整地满足土条力和力矩平衡方程，采用正弦条间力方向函数，计算精度较高，适用于有软弱夹层、薄斜墙坝、薄心墙坝及其他任何具有复杂土层结构的土工建筑。

• “斯宾塞法”

  与摩根斯坦-普莱斯法相同，仅在条间力方向函数的构造方面有所区别，斯宾塞法假设条间力方向恒定。

• “有限元强度折减法”

  基于结构有限元方法，通过迭代折减土体抗剪强度参数直至结构发生破坏导致非线性静力学计算发散的方式计算结构稳定临界状态。该方法可考虑多种静力学载荷，获得更准确的稳定性分析结果，但耗时较长。

• “超载法地震屈服加速度计算”

  基于结构有限元方法，通过迭代放大地震作用直至结构破坏的方式计算结构稳定临界状态。该方法用于计算大坝地震屈服加速度。

上述六种方法均支持导入渗流仿真分析得到的任意时间步所对应的渗流孔隙压力场。在V1.0软件中，仅有限元方法支持静水压力、淤沙压力、浪压力和地震作用的静力学载荷组合。用户需参考表 2，根据模型土层情况和精度要求选择合适的方法进行整体稳定分析。

建议：

1. 为提高计算效率，专家用户可凭借经验判断滑动面大致位置，采用极限平衡法粗略计算FS，再将此FS降低0.1~0.5作为强度折减法初始FS计算精确结果。
2. 为避免模型存在局部薄弱区或非线性计算设置不当导致有限元法过早发散而无法求解完整滑动面，可通过强度折减法粗略判断滑动面位置再采用刚体极限平衡法计算完整滑动面和相应的FS。
3. V1.0软件采用基于网格的LEM方法，实现渗流、稳定性和动力学求解器一体化兼容，因此建议使用中等或精细网格模型进行LEM计算，降低滑动面搜索误差。

此外，用户需注意中国标准(GB)和欧洲标准（CFBR）对整体稳定分析方法的要求和建议，前者推荐使用刚体极限平衡法，后者在此基础上允许使用有限元方法。

1. 材料

对于模型各区域，用户需在“力学材料参数”卡片中输入以下力学材料参数：

• 密度$(kg/m^3)$：用于计算重力作用。
• 弹性模量$(MPa)$：仅在有限元法中参与计算。
• 泊松比：仅在有限元法中参与计算。
• 摩擦角$(°)$：土体抗剪强度参数。
• 凝聚力$(kPa)$：土体抗剪强度参数。

此外，用户可通过激活“导入渗流孔隙压力场”选项，并在“导入时间步”参数中指定需导入的时间步（天），实现水力耦合计算。此功能要求用户在开始整体稳定分析之前已完成渗流仿真分析。稳态渗流情况用户无法做时间步选择。

2. 载荷

当且仅当使用有限元方法进行整体稳定分析时，用户可勾选并设置静水压力、淤沙压力、浪压力和地震作用四种静力载荷。

2.1 静水压力

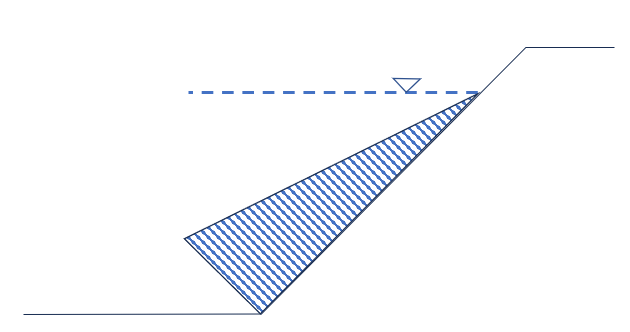
根据用户输入“上游水位”，软件计算大坝上游面静水压力载荷为：

$$P_w(y)={\rho }_{w}g\left(H_{am}-y\right)\text{\hspace{1em}(5)}$$

2.2 淤沙压力

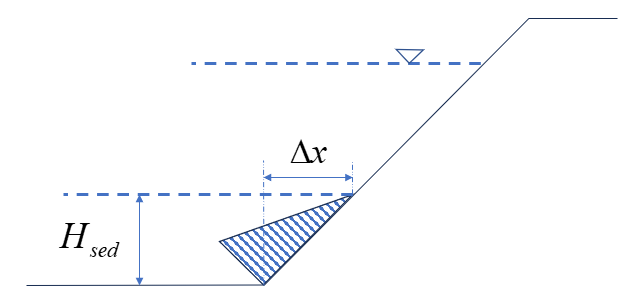
用户需输入：

• “淤沙浮容重” ${\gamma }_{sb}$ $(kN/m^3)$
• “淤积厚度” $H_{sed}$ $(m)$
• “淤沙内摩擦角” ${\varphi }_s$ $(°)$

其中淤沙浮容重可通过淤沙干容重 ${\gamma }_{sd}$ 和孔隙率 $n$ 计算：

$${\gamma }_{sb}={\gamma }_{sd}-(1-n){\gamma }_w\text{\hspace{1em}(6)}$$

淤沙压力分为水平力和竖向力，分别计算为：

$$\{\begin{array}{l}{P}_{sh}(y)={\gamma }_{sb}\left(H_{sed}-y\right){\tan }^2\left(45^{\circ }-{\varphi }_s/2\right)\\ P_{sv}(y)=-{\gamma }_{sb}\frac{\Delta x}{H_{sed}}\left(H_{sed}-y\right)\end{array}\text{\hspace{1em}(7)}$$

2.3 浪压力

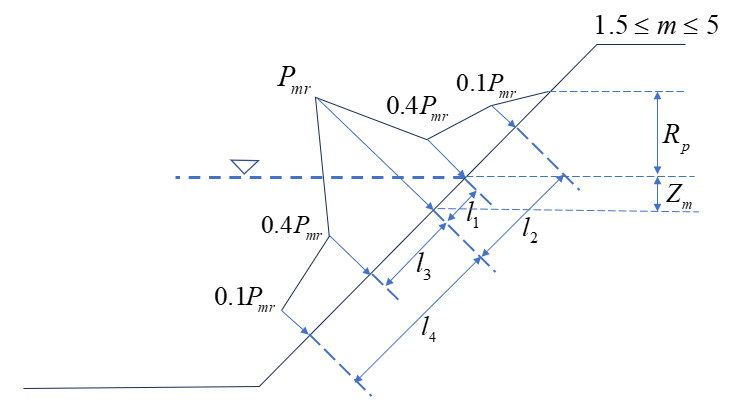
用户需输入：

• “波浪要素计算公式”

  根据水库具体条件，平原、滨海地区水库选择“莆田实验站公式”，丘陵、平原地区水库选择“鹤地水库公式”，内陆峡谷水库选择“官厅公式”。

• “风区长度”（$km$）：鹤地水库公式需<7.5 $km$，官厅水库公式需<20 $km$。

• “计算风速”（$m/s$）：鹤地水库公式需<26.5 $m/s$，官厅水库公式需<20 $m/s$。

• “平均水深”（$m$）：仅莆田实验站公式需设置。

• “糙率渗透性系数”：根据护面类型，参考表 3选取。

浪压力载荷在上游坡面表现为分布力，其中最大浪压力平均波浪爬高和最大浪压力作用点与水面垂直距离等参数根据GB/T 51394-2020《水工建筑物载荷标准》12.3.1节及附录H相关规定计算。

2.4 地震

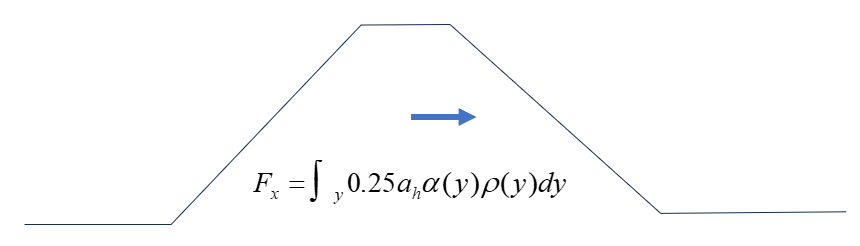
用户需输入：

• “水平峰值地震加速度” $a_h$ $(m/s^2)$

• “地震烈度”

  仅当“参考标准”选择中国标准（GB）时需输入，可选择设计烈度VII、VIII、IX度，用于计算地震惯性力动态分布系数。

当使用中国标准（GB）计算时，根据NB 35047-2015 《水电工程水工建筑物抗震设计规范》，软件以体积力形式计算地震惯性力：

$$E_i(y)=0.25\alpha (y)a_h\rho (y)\text{\hspace{1em}(8)}$$

其中地震惯性力动态分布系数 $\alpha (y)$根据坝高从坝基面至坝顶按线性（$H_{dam}\le 40m$）或双线性($H_{dam}>40m$)规律分布。

当使用欧洲标准（CFBR）时，地震惯性力动态分布系数与高程无关且固定为常值:

$$E_i=0.67a_h\rho \text{\hspace{1em}(9)}$$

注意：

当计算地震屈服加速度时，地震作用“水平峰值地震加速度”参数不参与计算，仅根据“地震烈度”计算动态分布系数。

3. 评价指标

当且仅当“行业规范”选择“电力行业标准”时，用户在“评价指标”选项卡中设置材料分项系数等评价指标计算抗滑稳定可靠度。输入参数包括：

• “抗剪强度分项系数”

  包括凝聚力 ${\gamma }_c$ 和摩擦系数 ${\gamma }_f$ 两个土体抗剪强度分项系数，一般情况下可取默认值 ${\gamma }_c=1.2$ 和 ${\gamma }_f=1.1$。

• “结构重要性系数” ${\gamma }_0$

  根据水工建筑物级别选取，1级取值1.1， 2、3级取值1.05，4、5级取值1.0。

• “设计状况系数” $\psi$

  根据工况类型选取，持久状况、短暂状况、偶然状况（1）和偶然状况（2）分别取值1.0， 0.95， 0.95， 0.85。工况定义参照NB/T 10872-2021 《碾压式土石坝设计规范》D.2小节。

软件根据NB/T 10872-2021标准中抗滑稳定安全裕度定义，定义抗滑稳定可靠度 $\eta$ 计算式为：

$$\eta =\frac{K_{\gamma }}{{\gamma }_0\psi }\ge {\gamma }_d\text{\hspace{1em}(10)}$$

其中 $K_{\gamma }$ 表示抗力与作用效应比， ${\gamma }_d$ 表示结构系数。结构系数代表大坝整体稳定安全阈值，特高坝选取1.3~1.35，其他取1.2。

4. 计算设置

根据不同计算方法，在“计算设置”选项卡中共有四种不同的整体稳定分析参数输入窗口。

4.1 瑞典圆弧法&简化毕肖普法

圆弧滑动面LEM方法中，用户需输入“土条数量”并定义滑动面搜索范围，满足计算基本要求。在“高级设置”选项卡中用户可对滑动面搜索算法和网格自动加密算法做进一步定义，提高求解精度和效率。

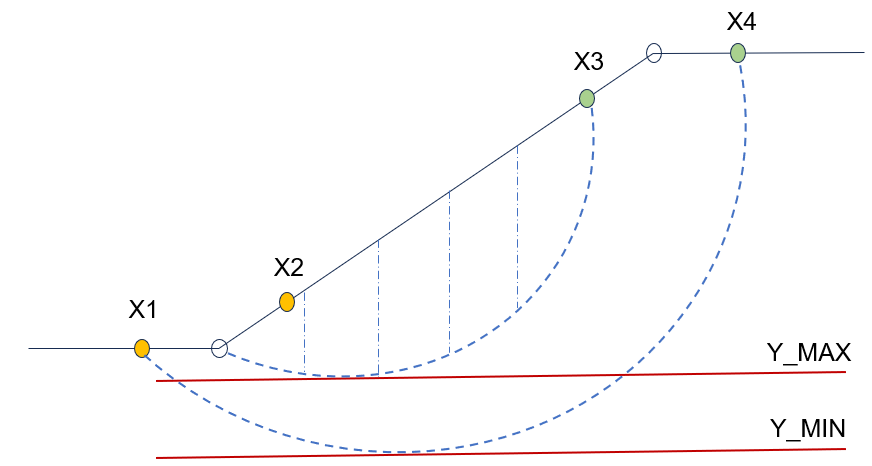
滑动面搜索范围定义参数包括：

• “滑动面左端点搜索范围X1”(m)：滑动面左端X坐标搜索域下限。
• “滑动面左端点搜索范围X2”(m)：滑动面左端X坐标搜索域上限。
• “滑动面右端点搜索范围X3”(m)：滑动面右端X坐标搜索域下限。
• “滑动面右端点搜索范围X4”(m)：滑动面右端X坐标搜索域上限。
• “滑动面左端搜索点数量”
• “滑动面右端搜索点数量”
• “水平切线最小值Y_MIN”（$m$）
• “水平切线最大值Y_MAX”（$m$）

其中搜索域端点定义需满足：

$$X_1\le X_2<{\mathrm{X}}_3\le X_4\text{\hspace{1em}(11)}$$

左右端搜索域根据搜索点数量均匀划分为潜在的滑动面端点，使得：

$$x_{l/r}^i=x_{l/r,min}+\left(x_{1/r,\max }-x_{l/r,\min }\right)/\left(N_{1/r}-1\right)i\forall i=0,1,\dots ,N_{1/r}-1\text{\hspace{1em}(12)}$$

滑动面搜索算法遍历全部潜在滑动面端点组合。对于各端点组合，算法自动计算滑动面半径搜索空间，选取步长 $dR=10\%H_{dam}$ 搜索最小化FS的最优滑动面，并在最优值附近采用二分法精确搜索滑动面半径最优解。

为了进一步提高计算效率或研究某一特定土层范围的滑动形态和稳定性系数，专家用户可通过定义水平切线范围手动划定滑动面半径搜索空间。对于端点组合，算法选取与Y_MIN和Y_MAX相切的两个滑动面半径作为搜索空间上下限。因此，水平切线的定义需满足：

$$y_{\text{min}}\le \min \left\{y_2,y_3\right\}\text{\hspace{1em}(13)}$$

其中 $y_2$、$y_3$ 分别表示X2和X3两点的Y坐标。

“网格自动加密算法”是针对滑动面搜索算法给出的最优滑动面，以网格节点到土条边缘的最小距离为判据，对土条边缘附近网格做迭代优化，从而降低或消除网格密度对FS计算结果的影响。用户需输入的参数包括：

• “最大加密次数”：一般可保留默认值4。
• “收敛误差”：判定FS收敛的最大误差范围，一般可保留默认值0.001。

4.2 摩根斯坦-普莱斯法&斯宾塞法

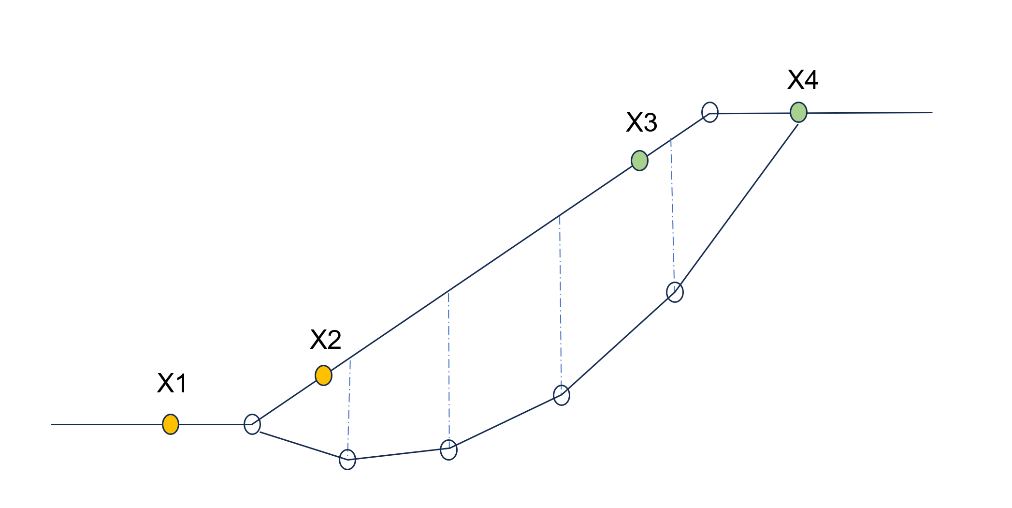
非圆弧滑动面LEM方法中，用户需输入“土条数量”，并定义滑动面端点搜索范围和群体优化算法基本参数。在“高级设置”选项卡中用户可对群体优化算法和网格自动加密算法做进一步精确定义，提高求解精度和效率。其中网格自动加密算法参数与圆弧滑动面LEM方法完全一致，滑动面端点搜索范围也采用先相同的方式定义。

非圆弧滑动面LEM方法与圆弧法的主要区别在于，由于折线形滑动面控制点数量不可控，优化算法状态变量总数取决于土条数量，因此采用增强烟花算法（Enhanced Firework Algorithm, EFWA）进行滑动面搜索。烟花算法（Firework Algorithm, FWA）是一种先进的群体优化算法，具有强大的全局并发搜索能力和良好的局部覆盖性，适用于多种优化问题。EFWA基于FWA在烟花爆炸和高斯火花生成算子与映射规则等方面做了改进，进一步强化了算法的局部搜索能力和适应性。V1.0软件在EFWA中加入滑动面控制点动态边界计算，确保滑动面运动学合理性并提升优化效率，同时采用轮盘赌方法进行烟花迭代筛选，形成具有动态约束条件的改进EFWA。

EFWA需输入的必要参数包括：

• “爆炸范围A”(m)

  爆炸火花的总辐射范围，可根据下式估算:

  $$A=\frac{M}{N_{\text{slice }}}{H}_{dam}\text{\hspace{1em}(14)}$$

  其中 $N_{slice}$ 表示土条数量， $H_{dam}$ 表示坝高。

• “边缘裕度”（m)

  滑动面距离模型边缘的最小距离。该参数用于避免滑动面与模型边缘距离过小导致土条内无法形成完整网格单元而计算出错，一般可选取最大网格尺寸的1.5~2倍作为边缘裕度。

• “根据当前结果续算”

  激活该选项时，程序自动读取当前计算结果作为本次计算初始烟花种群中的一个个体，在此基础上继续优化。续算功能要土条数量保持不变，且当前结果滑动面端点包含在本次计算滑动面端点搜索范围之内。

提示：

对于复杂土层土工结构，EFWA搜索全局最优解所需迭代次数较多耗时较长，且不容易确定合适的搜索范围、最大迭代次数和爆炸范围等参数，利用续算功能可分阶段计算，及时调整EFWA参数并缩小搜索范围。

此外，在“高级设置”选项卡中用户可调整的EFWA参数包括：

• “烟花数量N”：每一个烟花种群中的烟花数量，一般可保留默认值5。

• “火花数M”：烟花种群爆炸产生的火花总数，一般可保留默认值40。

• “高斯火花数MG”

  烟花种群爆炸产生的高斯火花总数。高斯火花的作用是产生种群变异，增强算法的全局搜索能力，一般可保留默认值5。

• “火花数下限系数SA”：用于控制烟花爆炸产生的最小火花数量，一般可保留默认值0.04。

• “火花数上限系数SB”：用于控制烟花爆炸产生的最大火花数量，一般可保留默认值0.8。

• “最大迭代次数”：EFWA最大种群迭代次数。

• “收敛误差”：判断EFWA优化过程收敛的最大FS误差范围。

• “稳定迭代次数”：判定EFWA优化过程收敛前FS变化量连续保持在“收敛误差”之内的次数。

其中“最大迭代次数”、“收敛误差”和“稳定迭代次数”是控制EFWA计算时间的关键参数，减小“最大迭代次数”和“稳定迭代次数”并增大“收敛误差”将使EFWA计算时间减小，但计算精度减低，滑动面和FS计算结果不准确，反之亦然。

4.3 有限元强度折减法

SRM方法中，用户需输入基本设置项：

• “计算区域”

  “上游坝坡”或“下游坝坡”。在V1.0软件中，下游坝坡稳定性计算在全模型区域进行强度折减；上游坝坡稳定性计算时软件自动识别坝顶下游侧顶点左侧区域，在该区域内进行强度折减。

• “载荷列表”

  “荷载”选项卡勾选的载荷中，用户可选择全部施加（“全选”），或全不施加（“不选”），抑或只施加四种载荷类型中其中一种。

• “初始稳定性系数”

  SRM计算区域内材料抗剪强度参数的初始折减系数。在缺少参考值的情况下一般取值为1.0。

• “计算精度” $p_{fin}$

  FS结果的计算精度，表示最终计算结果与非线性有限元计算发散的真实临界值之间的最大误差。

此外，用户可在“高级设置”选项卡中进一步精细化设置非线性有限元计算参数和折减系数迭代方法。非线性计算设置项包括：

• “时间步自动划分层数”

  在SRM算法中，力学载荷逐步加载，当某一时间步计算发散时则程序自动划分4个子步。该参数定义在同一时间步及其子步中自动划分子步的最大次数。要求该参数大于等于2，为确保计算精度，建议取值4。

• “最大迭代次数”

  非线性有限元计算每个时间步的最大牛顿-拉弗森迭代次数，建议取值30。

• “最大收敛残差” $\eta$

  非线性有限元计算全局最大容差，用于判定计算收敛性，具体定义为：

  $$\frac{{\Vert {\mathbf{Q}}^T\cdot {\mathbf{\sigma }}_i^n-{\mathbf{L}}_i^{\text{meca}}\Vert }_{\infty }}{{\Vert {\mathbf{L}}_i^{\text{meca}}+{\mathbf{L}}_i^{\text{varc}}\Vert }_{\infty }}\le \eta \text{\hspace{1em}(15)}$$

其中分子表示全局最大绝对容差，分母表示渗流孔隙压力和其他力学外载荷特征量。最大收敛残差建议取值1e-12，一般不大于1e-6。

除非线性有限元计算的收敛性之外，外层迭代的SRM算法收敛性由材料抗剪强度参数的折减系数的精细化迭代控制。折减系数迭代方法的设置参数包括：

• “初始稳定性系数增量” $p_0$

  材料抗剪强度参数初始折减系数增量，要求：

  $$p_0\ge p_{fin}\text{\hspace{1em}(16)}$$

• “稳定性系数渐进规律”

  材料抗剪强度参数折减系数增量的精细化渐进规律，可选“指数”或“线性”。

• “线性渐进迭代次数 $N$

  当“稳定性系数渐进规律”选择为“线性”时，定义材料抗剪强度参数折减系数增量由初始值 $p_0$ 减小至计算精度 $p_{fin}$ 所经历的步数。

• “最大迭代次数”：材料抗剪强度参数折减系数的最大迭代步数。

当选择指数渐进规律时，第n次增量精细化时新的增量计算为：

$$p_n=p_0{2}^{-n}\text{\hspace{1em}(17)}$$

当选择线性渐进规律时：

$$p_n=p_0-n\frac{p_0-p_{fin}}{N}\text{\hspace{1em}(18)}$$

用户需根据实际情况恰当选择指数或线性渐进迭代方法，当与相差较大时，建议选择指数渐进，反之选择线性渐进。选择线性渐进的判别关系式为：

$$\frac{p_0-p_{fin}}{{\log }_2\left(p_0\right)-{\log }_2\left(p_{fin}\right)}<N\text{\hspace{1em}(19)}$$

4.4 超载法地震屈服加速度计算

超载法地震屈服加速度计算与SRM方法类似，均采用非线性有限元计算发散作为结构失稳判别准则，区别在于屈服加速度计算中，由加速度系数代替SRM计算中材料折减系数进行迭代累加，实现地震惯性力的超载计算，直至计算发散。

地震屈服加速度系数定义为：

$$k_c=\frac{a_c}{g}\text{\hspace{1em}(20)}$$

其中 $a_c$ 表示使结构发生滑动失稳的临界水平加速度，$g$ 表示重力加速度。

屈服加速度计算要求必须在“荷载”选项卡中勾选地震作用，同时在使用“中国标准（GB）”时需设置“地震烈度”。屈服加速度计算不支持上下坝坡的选择。在“稳定性计算参数”设置窗口中的其余设置项与SRM方法相同。

5. 计算结果

根据不同的整体稳定分析方法，软件采用不同的结果展示方式。

• 瑞典圆弧法&简化毕肖普法

圆弧滑动面LEM方法计算结果包括滑动体可视化云图、稳定性系数、抗滑稳定可靠度（电力标准）、滑动面几何参数、已搜索滑动面统计和网格自动加密算法收敛曲线。

可视化云图中滑动体区域的值为1，其余部分值为0。

滑动面几何参数包括圆心坐标、滑动面半径和滑动面左右侧端点坐标。

已搜索滑动面统计展示优化算法计算过程中全部潜在滑动面的圆心坐标和半径的空间范围和滑动面总数，为用户判断结果合理性和可信度提供参考。

网格自动加密算法收敛曲线展示边缘网格迭代加密过程中FS的变化趋势，帮助用户判断算法收敛性和FS结果的准确度。

• 摩根斯坦-普莱斯法&斯宾塞法

非圆弧滑动面LEM方法的结果展示内容中，滑动体可视化云图和网格自动加密算法收敛曲线与圆弧法相同。

此外，在已搜索滑动面统计中，非圆弧法结果以曲线形式展示滑动面控制点坐标，光标悬浮在某一控制点，浮窗内展示控制点坐标具体数值及其在EFWA算法中的搜索空间上下限。

用户可根据增强烟花算法迭代优化曲线判断EFWA算法是否收敛，进而决定是否调整计算参数后续算。

• 有限元强度折减法&超载法屈服加速度计算

基于结构有限元方法的整体稳定分析计算结果展示滑动体云图、稳定性系数/屈服加速度系数、抗滑稳定可靠度（SRM电力标准）和稳定性系数/屈服加速度系数迭代曲线。

滑动体云图展示物理量为积累塑性应变，高值区代表土体局部剪切破坏的发生位置，可形成明显的塑性贯通区，表征边坡失稳潜在滑动面。某些特殊情况下可能无法观察到完整的塑性贯通区，一般由土层结构复杂、网格密度不足、非线性计算参数或SRM计算参数设置不合理导致。

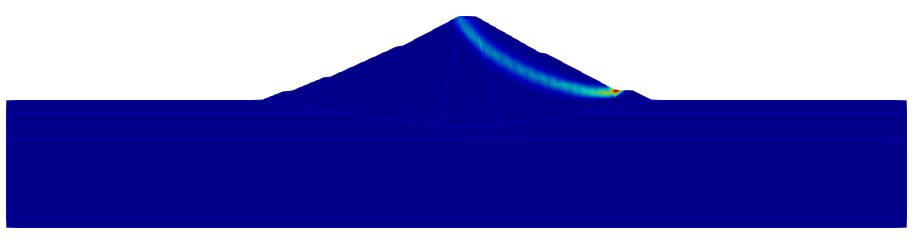
稳定性系数/屈服加速度迭代曲线描述FS/屈服加速度随计算区域最大总位移的变化关系，当FS/屈服加速度达到土体滑动失稳的临界值时可观察到总位移的突变，作为判断SRM/超载法屈服加速度计算收敛性判断的重要依据。

动力学时程分析

地震对土石坝等土工结构的损伤作用主要表现为过大的永久变形导致防渗系统损伤和破坏、坝体出现裂缝、安全超高不足等问题，以及边坡滑动体的永久变形导致边坡滑移失稳。动力学时程分析模块集成了无质量坝基模型、平面波模型等地震动输入模拟技术，支持Iwan非线性弹塑性动力学本构模型模拟土体动剪模量衰减特性，以及Newmark永久变形计算后处理功能，用于预测土工结构抗震动力学响应，预见可能的损伤区域和损伤程度，评估结构抗震稳定性。

地震永久变形分析需首先通过整体稳定分析地震屈服加速度计算得到边坡滑动体几何参数和屈服加速度系数，结合动力学时程分析得到的大坝加速度场时间历程计算滑动体永久变形和稳定性系数时程曲线。

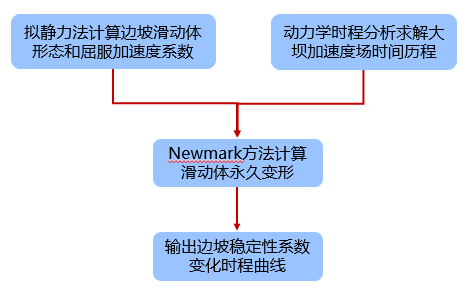
动力学时程分析计算设置参数包括材料设置、计算设置和后处理设置。

1. 材料

在“材料”选项卡中，用户需输入模型各土层弹性力学材料参数、抗剪强度参数，具体包括：

• 密度（kg/m3）
• 弹性模量（MPa）
• 泊松比
• 摩擦角（°）
• 凝聚力（kPa）

此外，用户还需输入动力学时程分析所需的模型个土层材料阻尼参数，支持同时输入模态阻尼比和瑞利阻尼相关参数，在后续计算设置中选择其一参与计算。

模态阻尼需为各土层设置：

• “振型阻尼比”

  常值模态阻尼比 $\xi$ ，定义为：

  $$\xi =\frac{\eta }{2}=\frac{E_{d,cycle}}{4\pi E_{p,max}}\text{\hspace{1em}(21)}$$

其中为 $\eta$ 损失系数，表示一个振动周期耗散能与 $2\pi$ 倍最大变形势能的比值。例如，振型阻尼比取值0.02，表示每个振动周期发生2%的振幅衰减。

瑞利阻尼需为各土层设置阻尼模型参数：

• “ $\alpha$ ”（ $s^{-1}$ ）
• “ $\beta$ ”（ $s$ ）

动力学方程中阻尼矩阵计算为：

$$\mathbf{C}=\alpha \mathbf{M}+\beta \mathbf{K}\text{\hspace{1em}(22)}$$

对于固有原频率为 ${\omega }_i$ 的第 $i$ 阶模态，瑞利阻尼和模态阻尼比具有如下换算关系：

$$\xi =\frac{\alpha }{2{\omega }_i}+\frac{\beta {\omega }_i}{2}\text{\hspace{1em}(23)}$$

在V1.0软件中，模态阻尼参数为常值阻尼，表示全模态的平均阻尼特性，在实际计算时根据用户输入加速度谱的频率区间自动计算所对应的瑞利阻尼参数。频率区间的确定方法为：将加速度做快速傅里叶变换，频率区间定义为幅值高于频谱最大幅值的20%的区间，区间端点圆频率定义为 ${\omega }_1$ 和 ${\omega }_2$。

通过求解方程组计算常数模态阻尼比对应的瑞利阻尼参数：

$$\{\begin{array}{l}2\xi =\frac{1}{{\omega }_2-{\omega }_1}{\int }_{{\omega }_1}^{{\omega }_2}\left(\frac{\alpha }{\omega }+\beta \omega \right)d\omega \\ \frac{\alpha }{{\omega }_1}+\beta {\omega }_1=\frac{\alpha }{{\omega }_2}+\beta {\omega }_2\end{array}\text{\hspace{1em}(24)}$$

2. 计算设置

在“计算设置”选项卡中用户可选择动力学时程分析所使用的阻尼模型，导入地震加速度谱，选择动力学本构模型，以及设置边坡永久变形计算参数。

在“阻尼”选项中用户可通过列表选择“瑞利阻尼”或“模态阻尼”。

2.1 地震动输入

在“地震动输入”窗口中，用户需导入地震加速度谱，对加速度谱做修正，同时完成写入时间步和地震动输入算法的相关设置。加速度谱输入采用CSV格式，需严格按照模板（点击“下载模板”按钮下载）规定格式输入数据，点击“上传”按钮导入加速度谱，随即可在上方曲线图预览加速度谱时域波形，在下方表格检查具体数据。

加速度谱中可同时提供水平和竖直方向加速度，用户可通过勾选“加速度谱修正”，在设置窗口中分别对两个方向的加速度谱设置修正参数：

• “放大倍数”：地震加速度输入的放大系数。

• “滤波截至频率” (Hz)

  高通滤波器的截止频率，用于消除加速度谱偏置量，在使用Iwan非线性模型进行时间积分时尤其重要，有效避免计算错误，建议取值0.05Hz。

在“写入时间步设置”选项卡中，可选择“写入时间步”的写入模式，包括:

• “按计算时间步写入”

  展示结果中包含加速度谱CSV文件中的全部时间步。

• “等间隔步数写入”

  将加速度谱CSV文件中的时间步按间隔步数重采样作为计算结果的时间步列表。

当选择“等间隔步数写入”时，需设置：

• “写入间隔步数”：重采样的间隔步数。

在“地震动输入算法设置”选项卡中，用户需指定“地震动输入算法”，共有两种模型选择：

• “无质量地基模型”

  将坝基质量自动设为0，即不考虑土基辐射阻尼产生的能量耗散，地震波输入均匀作用于坝基边界。该模型可同时考虑水平和竖直方向加速度谱。

• “平面波模型”

  通过计算平面地震波在地基中的传播模拟地震动载荷，充分考虑土基辐射阻尼，并采用傍轴近似粘弹性人工边界消除地基边界的反射波。

“平面波模型”仅支持单一方向的地震动输入，且定义地震波传播方向为Y轴正向。因此需用户选择：

• “平面波类型”

  压缩波(P波)或剪切波（S波）。前者对应Y方向加速度谱输入，后者对应X方向。

2.2 Iwan非线性动力学本构模型

Iwan弹塑性动力学本构模型是一种先进的岩土材料模型，相比于传统的等效线性模型能够充分考虑土体在地震循环载荷激励下的剪切模量衰减和随动硬化规律，提高土工结构地震动力学响应的数值计算精度。

Iwan模型由由若干串联的詹金斯单元（Jenkins element）构成，每个詹金斯单元包含并联的弹簧和滑块，从而组成“串联-并联”系统。当土体应力强度超过詹金斯单元屈服强度时，单元发生随动硬化使得应力状态保持在屈服面上。单元随动硬化率根据土体动剪模量关于动剪应变的关系曲线确定，使得模型能够反映土体动剪模量衰减特性。此外，伊万模型的构造方式天然地满足马辛准则，能够准确模拟土体应力应变滞回曲线。

詹金斯单元的数量和性质，及模型屈服面数量和分布，决定了模型对土体循环载荷激励下的力学行为的模拟精度，屈服面数量越多模拟精度越高，但计算时间复杂度也随之升高。因此V1.0软件固定使用12个屈服面的Iwan模型，定义其屈服剪应变覆盖1e-5~0.1的范围，从而适用于绝大部分土石坝地震工况。

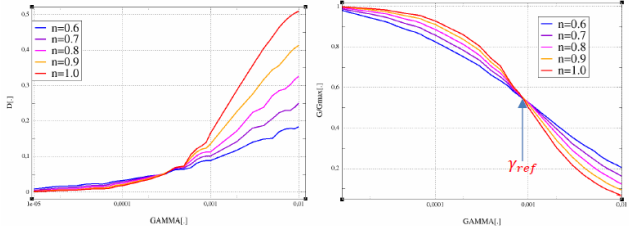
在V1.0软件中，Iwan模型只赋予坝体区域，坝基仍采用线弹性模型。

使用Iwan模型时需将“动力学本构模型”选项由“线弹性模型”切换至“Iwan弹塑性模型”，并在“Iwan弹塑性模型设置”窗口中设置坝体区域的模型参数，包括：

• “参考剪应变” ${\gamma }_{ref}$
• “幂指数” $n$

两个参数用于描述土体动剪模量 $G$ 随动剪应变 $\gamma$ 的变化规律：

$$\frac{G}{G_{\text{max }}}=\frac{1}{1+{\left(\gamma /{\gamma }_{ref}\right)}^n}\text{\hspace{1em}(25)}$$

提示：

1. Iwan模型参数需根据实际土料的试验曲线拟合确定。
2. Iwan模型考虑了滞回材料阻尼，计算得到的大坝动力学响应相比于无阻尼的线弹性模型显著偏弱，需根据实际情况调整瑞利阻尼或模态阻尼比，必要时将其置零。
3. 采用Iwan模型进行动力学时程分析计算时间较长，为确保收敛性，软件采用自动划分最多10级子步的时间步划分算法。

2.3 地震边坡稳定性动力学计算

计算边坡滑动体永久变形需用户勾选“地震边坡稳定性动力学计算”选项卡，并手动输入整体稳定分析中计算得到的边坡滑动体几何参数和屈服加速度。滑动体参数有两种输入方法，在“坐标输入类型”选项中切换：

• “圆心坐标输入”：需定义滑动面圆心X、Y坐标（$m$）和滑动面半径（$m$）。
• “端点坐标输入”：需定义滑动面左、右端点X坐标（$m$）和滑动面半径（$m$）。

此外用户需输入：

• “地震屈服加速度系数” $k_c$

  由整体稳定分析模块中通过“超载法地震屈服加速度计算”得到。

软件基于Newmark永久变形理论对动力学时程分析结果进行后处理，计算滑动体平均加速度、永久变形和稳定性系数时程曲线。

滑动体平均加速度计算式为：

$$a_m=\frac{F_x}{M}\text{\hspace{1em}(26)}$$

其中 $F_x$ 表示滑动体所受水平力，由滑动面垂直应力积分得到，$M$ 表示滑动体总质量。

根据Newmark理论，滑动体永久变形计算式为：

$$d_{irr}={\iint }_t\frac{1}{2}\left(1+\mathrm{sgn}\left(a_m(t)-a_c\right)\right)\left(a_m(t)-a_c\right)d^{2}t\text{\hspace{1em}(27)}$$

边坡稳定性系数包括仅在自重作用下的静力部分和地震载荷激励下的动力部分，通过滑动面应力积分得到，计算式为：

$$F{S}_d(t)=\frac{{\sum }_i^N\left(c^{\prime }+{\sigma }_n^{i,s}\tan \left({\varphi }^{\prime }\right)\right)\Delta L+{\sum }_i^N\left({\sigma }_n^{i,d}(t)\tan \left({\varphi }^{\prime }\right)\right)\Delta L}{{\sum }_i^N{\sigma }_t^{i,s}\Delta L+{\sum }_i^N{\sigma }_t^{i,d}(t)\Delta L}\text{\hspace{1em}(28)}$$

3. 后处理

在“后处理”选项卡中，用户可通过输入坐标或鼠标拾取定义最多5个兴趣点。点击“添加兴趣点”或“删除兴趣点”对兴趣点做增删修改。添加兴趣点后，在结果查看窗口中可查询各兴趣点位置位移、速度和加速度时程曲线。

4. 计算结果

动力学时程分析结果包含以下物理场的最大和最小场云图：

• 加速度 $(m/s^2)$ ：分为水平、垂直和总加速度。
• 速度 $(m/s)$ ：分为水平、垂直和总速度。
• 位移 $(m)$ ：分为水平、垂直和总位移。
• 应力 $(Pa)$ ：分为X和Y法向应力。
• 主应力 $(Pa)$ ：分为最大和最小主应力。

用户可通过点选“最大”或“最小”选项进行切换。此外，用户可查看最大剪应变云图，剪应变定义为：

$$\gamma =2{\epsilon }_{xy}\text{\hspace{1em}(29)}$$

若在“后处理”选项卡中定义了兴趣点，则可查看各兴趣点（否则默认展示坝顶上下游侧顶点）位置的以下物理量时程曲线；

• 加速度 $(m/s^2)$ ：分为水平、垂直和总加速度。
• 速度 $(m/s)$ ：分为水平、垂直和总速度。
• 位移 $(m)$ ：分为水平、垂直和总位移。

若用户在“计算设置”选项卡中勾选“地震边坡稳定性动力学计算”则可额外查看以下物理量时程曲线：

• 滑动体平均加速度 $a_m$ $(m/s2)$
• 滑动体永久变形 $d_{irr}$ $(m)$
• 边坡稳定性系数FS