断裂分析
断裂分析是工程学和材料科学领域的一项重要技术,它主要用于理解材料或结构在受力过程中裂纹形成和扩展的行为。这项分析旨在预测材料在不同条件下的断裂行为,从而帮助工程师评估和改进产品设计、预测寿命以及确保结构的安全性。
关键词:
裂纹的形成和扩展:裂纹是材料中的缺陷,可以是由于外部载荷、疲劳加载、环境因素或材料缺陷引起。分析通过模拟裂纹的形成和扩展来了解这一过程。
应力集中:裂纹周围的应力集中是裂纹扩展的关键因素。它导致局部应力增加,可能加速裂纹扩展。
数值模拟:通过数值方法(例如有限元分析)模拟结构在不同载荷条件下的应力、应变分布,以及裂纹的形成和扩展。
裂纹尖端应力场:断裂分析着重考虑裂纹尖端的应力场分布,因为这是裂纹扩展的关键位置。
裂纹扩展预测:通过对裂纹形态、材料性质和加载条件的建模,预测裂纹扩展速率和路径。
应用领域:断裂分析在建筑、航空航天、汽车等领域中用于评估结构的强度和耐久性,以确保安全和可靠性。断裂分析也用于材料疲劳性能评估和材料改进,以延长产品寿命。断裂分析还用于了解事故和材料损伤的原因,从而改进产品设计和安全标准。断裂分析在工程和科学领域中发挥着关键作用,帮助理解材料和结构在各种条件下的性能,从而指导产品设计和安全评估。
使用CAE365网站,我们可以通过下面的几个步骤轻松开启断裂分析仿真
进入CAE365网站
在页面下方模块栏中选择结构仿真-断裂分析,点击开始仿真按钮,开始仿真:
在弹出的创建工程窗口中输入工程名:
输入工程名称后,点击创建,进入断裂分析仿真界面:
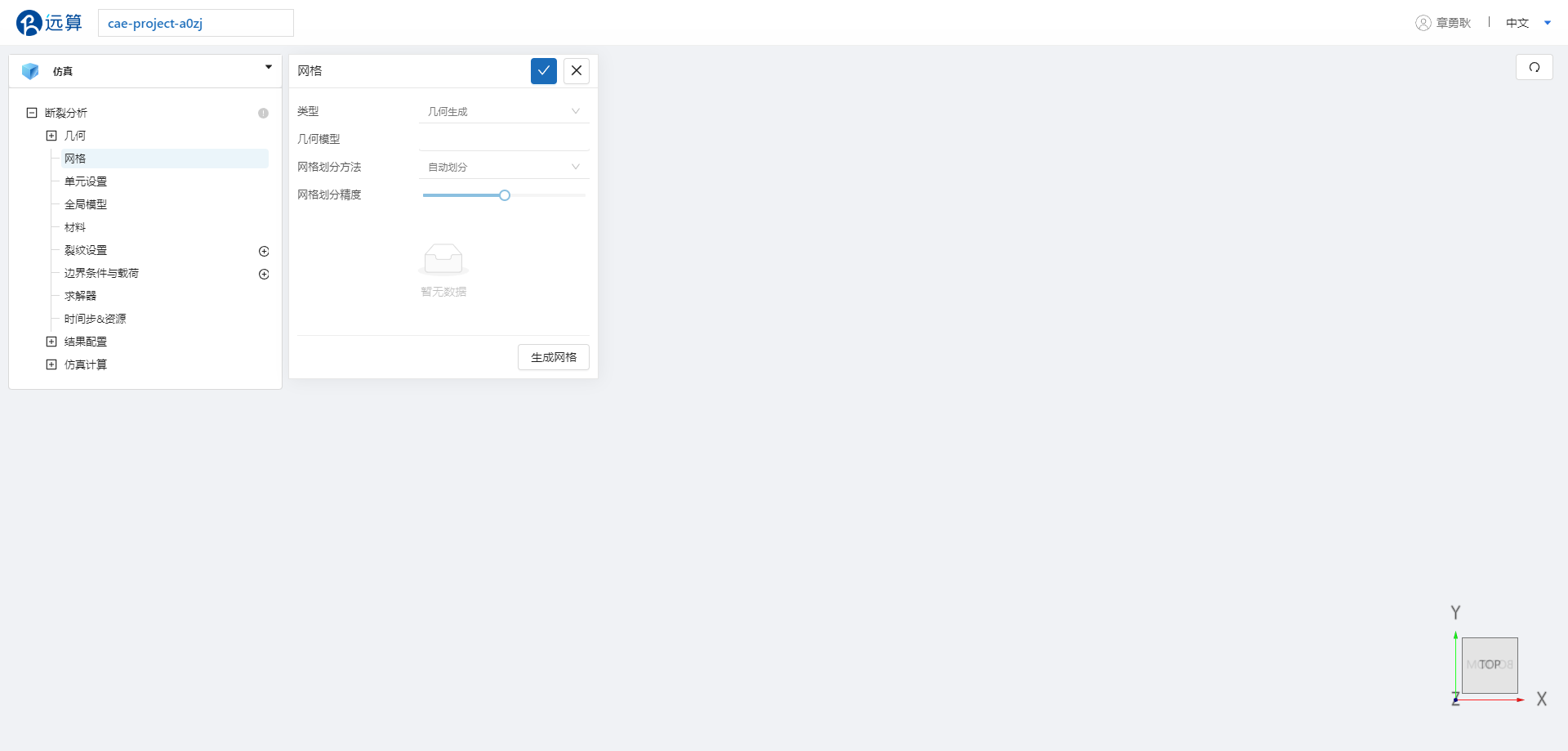
断裂分析仿真模块树如图所示:

1. 产品手册
1.1 几何导入
用户可以在这里上传几何模型,模型格式建议为iges、step、brep、xao且大小不超过200M。
1.1.1 几何分组
用户可以在几何模型中创建点、线、面、体的分组。
1.2 网格导入
用户可通过点击网格,导入本地网格,格式建议为,med、inp、cdb、cgns且大小不超过200M。用户需预先把所需的载荷组与约束组定义完整,否则在后续的仿真分析中不能选择未定义组的点、线、面和体。 同时可以在此选项按照平台内置算法划分网格。
1.3 单元设置
在此选项卡中,可手动或自动选择将惯性效应设置为二维和三维。其中2D包含平面应变模型、平面应力模型以及轴对称模型,3D单元类型为三维完全积分单元。
1.4 全局模型
在此选项卡中用户可以定义重力加速度的大小和方向,其中方向是由向量定义的。
1.5 材料设置
在此选项卡中,用户可设置材料的相关属性,密度、泊松比、杨氏模量,材料本构默认为线弹性材料。
1.6 裂纹设置
裂纹分为2D单元和3D单元。2D单元的裂纹类型包括线段和射线。3D单元的裂纹类型包括椭圆、矩形、圆柱和半平面。
1.7 边界条件与载荷
用户可在边界条件选项卡中选择约束类型和加载方式;
约束类型包括:固定支撑、位移约束、对称约束;
荷载类型包括:面分布荷载、体分布荷载、压强。
1.8 求解器
在此选项卡中,用户可根据自己的需要对求解器进行个性化选择与设置,以满足计算需求。用户可在求解器中选择不同的计算方法,选择不同的迭代方法和收敛准则。
1.9 时间步&资源
用户可设置计算的核数以及最大计算时间。
1.10 结果配置
在此选项卡中用户可以输出位移结果,结果以云图方式展示,同时用户还可得到计算时的求解日志,来获取计算时的一些重要信息,及错误提醒,方便用户及时找到问题所在,解决棘手问题。
2. 教程案例
3. 设置项详解
3.1 几何
用户可从本地上传几何文件,上传后选项卡会展示几何外形,显示顶点数量、边线数量、环线数量和面数量等。
- 几何分组:上传几何文件后,用户需对几何进行分组,以便在后续的仿真分析中选择所需的点、线和面。不分组自动画网格功能不能使用!
3.2 网格
用户可从本地上传网格文件,上传后选项卡会展示网格外形,显示单元数量、节点数量、边线数量和面数量等。上传网格文件前,用户需提前对模型进行分组,以便在后续的仿真分析中选择所需的点、线和面。
用户也可将上传的几何文件在此处划分网格,生成.med文件。
- 类型:在此处选择用于计算的网格来源
- 几何生成:将上传的几何文件剖分
- 上传网格:直接导入外部网格模型
- 几何模型:当类型处选择“几何生成”时,此处默认的是导入几何的文件名。
- 网格划分方法:此处选择划分网格的算法。
- 自动划分:平台自动生成四面体网格,只能调节网格密度。
- 手动划分:可以调节网格的单元最大最小尺寸以及网格密度
- 网格划分精度:控制网格密度的滑块,0代表网格最粗糙,4代表网格最精细。
- 单元最大尺寸:手动划分时,用户可以自定义单元的最大长度。
- 单元最小尺寸:手动划分时,用户可以自定义单元的最小长度。
3.3 单元设置
- 惯性效应:惯性效应通常指的是结构在受到快速加载或动态载荷时,由于质量分布和加速度而产生的力学效应。
- 3D:在三维模型中,惯性效应需要考虑三个方向的加速度和惯性力,这更加接近实际物理情况。
- 2D:在二维模型中,惯性效应通常被简化为平面内的质点运动,只考虑两个方向的加速度和惯性力。
- 单元类型:在选择单元类型时,需要考虑结构的几何形状、材料属性、加载条件以及分析目标。不同的单元类型具有不同的计算精度和计算成本,因此需要根据具体情况进行选择。同时,还需要注意单元之间的连接方式和边界条件的设置,以确保分析结果的准确性和可靠性。
- 三维完全积分单元:当“惯性效应”选择3D时,此处为默认选项。常指的是对单元刚度矩阵中的多项式项进行精确积分所需的单元类型。
- 平面应变模型:常用于模拟在某一平面内存在显著应力和应变变化,但在与该平面垂直的方向上应变非常小的结构或材料。
- 平面应力模型:用于模拟在某一平面内存在显著应力和应变变化,但在与该平面垂直的方向上应力为零的结构或材料。
- 轴对称模型:在有限元分析中是一种简化的模型,用于模拟具有轴对称性的物理系统或结构。
3.4 全局模型
全局模型:用户可在此选项卡中输入重力加速度,重力加速度输入的形式包括数值,表格或者函数形式,同时可在全局坐标系下定义重力加速度的方向,默认为Z的负方向。
3.5 材料
材料选项卡中用户可定义全局的材料性能,包括材料本构行为(默认线弹性),杨氏模量、泊松比、密度,单位也可根据需要随时改变。
3.6 裂纹设置
单元设置——惯性效应——2D
- 线段
- 裂纹类型:线段
- θ场变化区域内径:由用户设置根据几何尺寸设置的一个浮点数,用于控制裂纹扩展区域。
- θ场变化区域外径:由用户设置根据几何尺寸设置的一个浮点数,用于控制裂纹扩展区域,数值应比内径数值大。
- 裂纹起点坐标:用户通过三个坐标输入控制裂纹开始的位置。
- 裂纹终点坐标:用户通过三个坐标输入控制裂纹结束的位置。
- 射线:
- 裂纹类型:射线
- θ场变化区域内径:由用户设置根据几何尺寸设置的一个浮点数,用于控制裂纹扩展区域。
- θ场变化区域外径:由用户设置根据几何尺寸设置的一个浮点数,用于控制裂纹扩展区域,数值应比内径数值大。
- 裂纹尖端经过点坐标:用户通过三个坐标输入控制裂纹尖端的位置。
- 开裂方向:通过向量的方式控制裂纹开裂的方向。
单元设置——惯性效应——3D
- 椭圆
- 裂纹类型:椭圆
- θ场变化区域内径:由用户设置根据几何尺寸设置的一个浮点数,用于控制裂纹扩展区域。
- θ场变化区域外径:由用户设置根据几何尺寸设置的一个浮点数,用于控制裂纹扩展区域,数值应比内径数值大。
- 椭圆裂纹中心坐标:用户通过三个坐标控制椭圆裂纹的中心坐标。
- 椭圆半长轴半短轴长度
- a:用户设置一个浮点数定义半长轴的长度。
- b:用户设置一个浮点数定义半短轴的长度。
- 椭圆半长轴方向:通过向量的方式定义半长轴的方向。
- 椭圆半短轴方向:通过向量的方式定义半短轴的方向。
- 开裂区域:定义裂纹的位置是在模型内部还是模型外部。
- 内部
- 外部
- 矩形
- 裂纹类型:矩形
- θ场变化区域内径:由用户设置根据几何尺寸设置的一个浮点数,用于控制裂纹扩展区域。
- θ场变化区域外径:由用户设置根据几何尺寸设置的一个浮点数,用于控制裂纹扩展区域,数值应比内径数值大。
- 矩形裂纹中心坐标:用户通过三个坐标控制矩形裂纹的中心坐标。
- 矩形尺寸
- 半长度:用户设置一个浮点数定义矩形长度的一半。
- 半宽度:用户设置一个浮点数定义矩形宽度的一半。
- 倒角半径:用户设置一个浮点数定义矩形裂缝的四个倒角的半径。
- 矩形长方向:通过向量的方式定义矩形长的方向。
- 矩形款方向:通过向量的方式定义矩形宽的方向。
- 开裂区域:定义裂纹的位置是在模型内部还是模型外部。
- 内部
- 外部
- 圆柱
- 裂纹类型:圆柱
- θ场变化区域内径:由用户设置根据几何尺寸设置的一个浮点数,用于控制裂纹扩展区域。
- θ场变化区域外径:由用户设置根据几何尺寸设置的一个浮点数,用于控制裂纹扩展区域,数值应比内径数值大。
- 圆柱裂纹椭圆面中心坐标:用户通过三个坐标控制圆柱裂纹椭圆面的中心坐标。
- 圆柱裂纹椭圆面半长轴半短轴长度
- a:用户设置一个浮点数定义半长轴的长度。
- b:用户设置一个浮点数定义半短轴的长度。
- 圆柱裂纹椭圆面半长轴方向:通过向量的方式定义半长轴的方向。
- 圆柱裂纹椭圆面半短轴方向:通过向量的方式定义半短轴的方向。
- 半平面
- 裂纹类型:半平面
- θ场变化区域内径:由用户设置根据几何尺寸设置的一个浮点数,用于控制裂纹扩展区域。
- θ场变化区域外径:由用户设置根据几何尺寸设置的一个浮点数,用于控制裂纹扩展区域,数值应比内径数值大。
- 裂纹尖端经过点坐标:用户通过三个坐标控制裂纹尖端的坐标。
- 断裂面法向:通过向量的方式控制断裂面的法向方向。
- 开裂方向:通过向量的方式定义裂纹开裂的方向。
3.7 边界条件
边界条件定义了结构的支撑情况和结构与外部环境的相互作用,点击边界条件与载荷旁的加号按钮可选择不同的边界类型:
- 面分布载荷
- 边界类型:面分布载荷
- 面分布载荷:用户可在此处自定义三个方向的分量值,数值可通过直接输入值、表格输入、公式输入三种方式输入;
- 施加位置:选取载荷所作用的位置。
- 体分布载荷
- 边界类型:体分布载荷
- 体分布载荷:用户可在此处自定义三个方向的分量值,数值可通过直接输入值、表格输入、公式输入三种方式输入;
- 施加位置:选取载荷所作用的位置。
- 压强
- 边界类型:压强
- 压强:用户可在该选项卡中选择需要的面单元施加压强,压强方向默认为施加平面的内法线方向,数值可通过直接输入值、表格输入、函数输入三种方式输入;
- 施加位置:荷载所作用的位置。
- 固定支撑:用户可在该选项卡中选择需要的体、面、线、点,施加6个自由度方向的固定约束;
- 位移约束:用户可在该选项卡中选择需要的体、面、线、点,施加3个平动自由度的位移,可通过勾选对应方向的选择框来自由选择所需方向的位移条件,数值可通过直接输入值、表格输入、函数输入三种方式输入;
- 对称约束:用户可在该选项卡中选择需要的面,该平面作为结构的对称平面;
3.8 求解器
求解器面板包含控制方程求解器的一些设置,这些参数在大多数情况下都足够好,但用户可利用可选项来优化计算过程,提高速度、鲁棒性和精度。 求解计算方法包含:MUMPS,LDLT,Multifrontal,PETSC四种方法
- 检测到奇异时是否停止:打开则会开启评估,当矩阵奇异性评估结果为正,则停止计算,对于非线性解,可用牛顿准则代替。
- 奇异性检测精度:设置矩阵奇异性评估的数值精度,如果设置负值则关闭监测
- 网格细化:由用户决定是否打开此选项,此功能可以使裂纹计算更加精细。
- 细化迭代数:由用户设置一个整数,来定义对裂纹处网格细化的次数。
- 细化区域半径:由用户设置一个浮点数,来定义细化网格的范围。
- 粗化区域半径:由用户设置一个浮点数,来定义细化网格的范围。建议数值与细化区域半径保持一致。
MUMPS多用于大规模稀疏矩阵的直接求解,该选项卡有自己的一些特定设置
- 矩阵优化内存分配率:用于数据透视操作估计量之上保留的内存比例设定
- 是否进行预处理:用户可选择是否启用矩阵的预分析用以优化计算
- 矩阵重新编号方法:矩阵优化算法,对仿真计算的内存消耗有巨大影响:
- AMD:使用近似最小度数方法
- SCOTCH:是一个强大的重新编号工具,适用于大多数场景,是MUMPS的标准选项
- AMF:使用近似最小填充方法
- PORD:是MUMPS中包含的重新编号工具
- QAMD:是自动检测准密集矩阵的AMD变体。
- Automatic: MUMPS自动选择重新编号的方法
- 分布式矩阵存储:如果启用,矩阵存储将在不同的进程中拆分,禁用则为每个进程保存一份矩阵副本
- 内存管理:允许选择RAM与磁盘的使用情况
- 自动:允许求解器决定最佳设置
- 核内存储:通过将所有对象存储在内存中,优化计算时间。
- 评估:在求解器日志中提供最佳设置
- 核外存储:通过在内存外存储对象来优化内存使用
- 矩阵类型:用于判断计算时采用的矩阵结构。
- 自动检测:系统默认选项,建议使用。
- 非对称矩阵
- 对称不定矩阵
- 对称正定矩阵
- 相对残差收敛阈值:用于判断计算时的收敛准则,可由用户根据计算结果要求的精确性自主更改。数值越大,计算越容易收敛,但是结果精度越低,一般推荐1e-5。
- 迭代求解后处理:系统默认自动,建议使用默认设置。
- 自动
- 启用
- 停用 LDLT对系数矩阵执行经典的高斯消去过程
MULTIFRONTAL系数矩阵分解法对矩阵进行LU或Cholesky分解,该方法的矩阵重新编号方法有两种方法
- MDA:对超过5000或者更大自由度的大模型选择此选项
- MD:小模型选择此选项
PETSC使用可移植、可扩展的科学计算工具包中的不同算法和组件。
- 矩阵优化内存分配率:用于数据透视操作估计量之上保留的内存比例设定
- 相对残差收敛阈值:用于判断计算时的收敛准则,可由用户根据计算结果要求的精确性自主更改。数值越大,计算越容易收敛,但是结果精度越低,一般推荐1e-5。
- 分布式矩阵存储:如果启用,矩阵存储将在不同的进程中拆分,禁用则为每个进程保存一份矩阵副本。
- 算法:选择求解算法
- CG:共轭梯度
- CR:共轭残差
- GCR:广义共轭残差
- GMRES:最小广义残差,是鲁棒性和速度之间的最佳折衷
- 预处理器类型:选择算法以计算和重新调整矩阵用以寻找最优解
- MUMPS LDLT:单精度完全Cholesky分解
- Incomplete LDLT:是另一种针对对称矩阵的分解方法,但与Cholesky分解不同。
- Jacobi:Jacobi迭代法是一种用于求解线性系统的迭代方法。它基于矩阵的分裂(通常是将矩阵分解为对角矩阵和剩余部分),并在每一步中通过求解对角方程来更新解。这种方法在某些情况下可以快速收敛,但通常不如其他更复杂的迭代方法(如SOR)稳健。
- SOR:SOR是另一种用于求解线性系统的迭代方法。它是Gauss-Seidel方法的改进版本,通过引入一个称为松弛参数的额外参数来加速收敛。
- Inactive:不激活预处理器。
- 预处理器矩阵刷新间隔:设定矩阵迭代刷新间隔。
- 最大迭代次数:求解器允许的最大迭代次数。如果设置为0,则按算法执行值估计。
3.9 时间步&资源
在此选项卡中,用户可设定计算所需的资源和计算时间;
- 计算核数:定义仿真计算所需的计算核数;
- 最大计算时间:定义仿真的最大时间,超过该值就会自动停止计算。
3.10 后处理
在此选项卡中,用户可输出响应的结果;
- 物理场:可选择输出结果,包括位移、应力(柯西应力、冯米塞斯应力)、应变、力(节点力、节点反力)。
3.11 仿真结果
用户可在此选项卡中获得仿真计算之后的云图,而且可获得计算日志,便于用户的使用,同时当全部条件设定完成后可在本选项卡处点击开始计算按钮,会给用户显示项目的创建时间和结束时间。
