入门案例
1. 案例简介
本案例使用远算大坝设计仿真一体化软件-土石坝仿真设计软件分析某粘土心墙土石坝渗流稳定、整体稳定和抗震稳定性。本案例旨在帮助用户理解软件参数设置和交互逻辑,体验大坝仿真设计全流程,大坝形体、材料和计算参数均在合理范围内虚构,因此计算结果不可与工程实际关联解读。
1.1 大坝基本信息
我国西部某水库拦河坝为粘土心墙砂壳坝,粘土心墙齿槽深入基岩内,坝顶上游侧设混凝土防浪墙,心墙上下游坝壳为砂砾石,同时在下游坝脚设堆石区。大坝按100年一遇洪水进行设计,坝顶高程94.2m,最大坝高41.5m,坝顶长535m,顶宽6.4m。上游坝坡分为三级坡度,分别为1:1.92、1:2.2和1:2.3,相应高程81.18m和68.18m处设2m宽马道;下游坝坡也分为三级坡度,分别为1:1.765、1:1.9和1:2,在78.18m处设2m宽马道,下游62.18m处设7.6m宽平台。心墙上下游坡比均为0.3。大坝设计地震烈度为VIII级。
1.2 仿真建模
本案例所涉及的软件功能和步骤如下:
-
几何网格模型搭建
根据大坝基本信息提取大坝坡面轮廓线,使用心墙坝参数化快速建模功能绘制砂壳、心墙、和分层坝基,忽略防渗墙结构。
-
瞬态渗流仿真分析
模拟库水位由正常蓄水位83.18m在4天内降落至枯水位53.18m的非匀速水位骤降过程中渗透稳定关键指标的变化过程。
-
整体稳定分析
分别采用简化毕肖普法和有限元强度折减法分析正常蓄水位工况下游边坡稳定性,对比滑动面和稳定性系数结果,形成相互校验。根据电力行业规范进行稳定性安全校核。最后计算地震屈服加速度,用于永久变形计算。
-
动力学时程分析
以"El Centro"地震波作为地震动输入,使用平面波模型和线弹性本构模型计算大坝2s内的动力学响应,并计算滑动体永久变形评估大坝抗震稳定性。
2. 软件操作流程
2.1 参数化建模和网格绘制
-
步骤1:几何绘制
在“建模方式”选项卡中选择“参数化建模”,点击打开“几何设置”窗口,分别在“大坝轮廓”和“心墙”表格中输入如表1、表2所示的模型参数。心墙高度约44米,嵌入坝基,心墙顶与坝顶不重合。
为了避免模型中局部材料抗剪性能的突变使得后续基于有限元强度折减法的稳定性分析结果产生偏差,此处取消勾选“防渗墙”。创建4层坝基,在“坝基分层”表格中依次输入左端高程-10, -16, -50(m),以及右端高程-3, -20, -50(m)。
至此,可在上方几何预览窗口中检查校对大坝几何参数正确性,无误则点击“生成几何”按钮生成大坝几何。
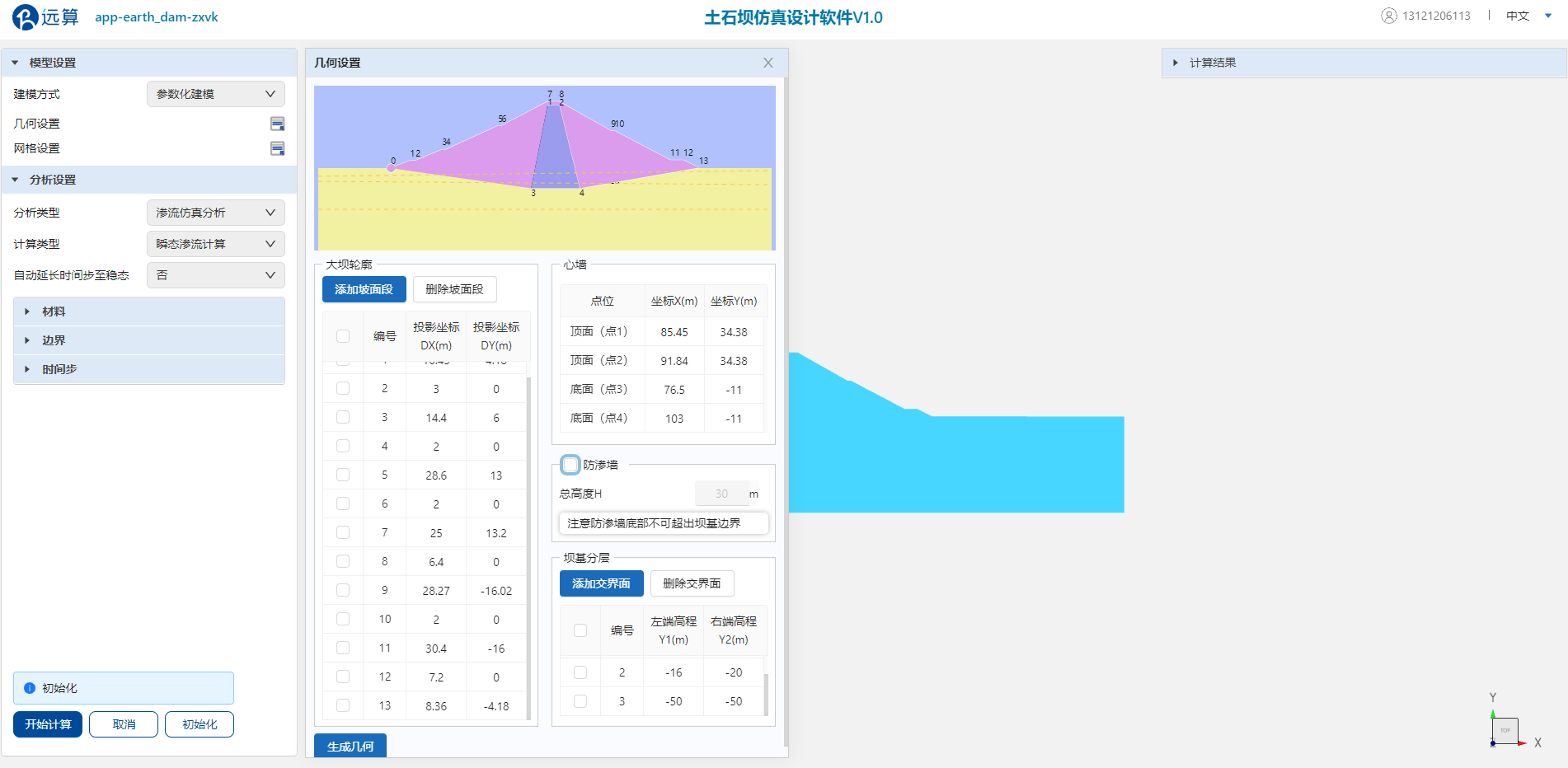
几何模型参数输入界面
表1 坡面线投影参数表
| 编号 | 投影坐标DX(m) | 投影坐标DY(m) |
|---|---|---|
| 1 | 10.45 | 4.18 |
| 2 | 3 | 0 |
| 3 | 14.4 | 6 |
| 4 | 2 | 0 |
| 5 | 28.6 | 13 |
| 6 | 2 | 0 |
| 7 | 25 | 13.2 |
| 8 | 6.4 | 0 |
| 9 | 28.27 | -16.02 |
| 10 | 2 | 0 |
| 11 | 30.4 | -16 |
| 12 | 7.2 | 0 |
| 13 | 8.36 | -4.18 |
表2 心墙坐标参数表
| 点位 | 坐标X (m) | 坐标Y(m) |
|---|---|---|
| 顶面(点1) | 85.45 | 34.38 |
| 顶面(点2) | 91.84 | 34.38 |
| 底面(点3) | 76.5 | -11 |
| 底面(点4) | 103 | -11 |
-
步骤2:网格划分
打开“网格设置”窗口,将砂壳和心墙网格特征尺寸设置为3(m),坝基各层分别设置为3、5、10、10(m)。点击“生成网格”生成大坝网格模型。
此处网格特征尺寸参数表示各区域的最大网格单元尺寸,心墙和砂壳网格较密,满足有限元计算网格无关性,从第二层坝基开始逐渐放大单元尺寸,在保证网格尺寸连续性的前提下降低网格总数,加快计算速度。
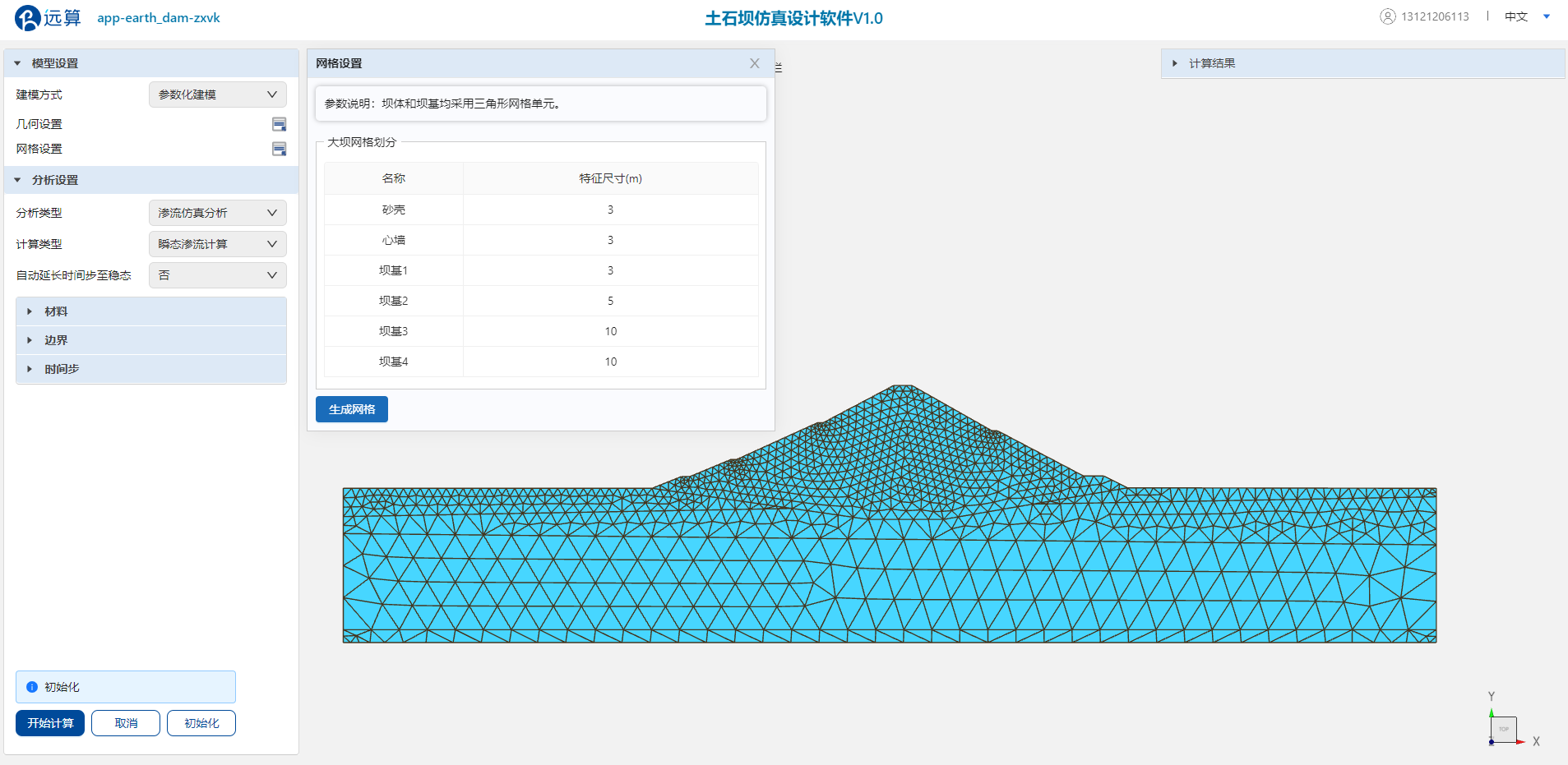
大坝网格模型生成结果
2.2 瞬态渗流仿真分析
-
步骤1:计算模型设置
在“计算设置”选项卡中,选择“分析类型”为“渗流仿真分析”,“计算类型”选择“瞬态渗流计算”。为了加快计算速度,将“自动延长时间步至稳态”选为“否”。
自动延长时间步至稳态的功能适用于瞬态渗流仿真分析。由于软件采用非饱和-非稳定渗流模型,当计算时间结束时,若空隙压力场仍处于非稳定状态,软件将自动延长计算时间并估算合适的时间步长继续计算,直到空隙压力场稳定,便于用户观察到由水位动态变化引起的渗流场演变全过程。
-
步骤2:水力学材料参数设置
打开“水力学材料参数”设置窗口,将"水的密度"设置为,“水动力学粘度”设置为,“比奥系数”设置为。其他材料参数如表3所示。
此处比奥系数和孔隙率在当前版本的渗流仿真中没有影响,在后续即将发布渗流-应力双向耦合仿真功能中,比奥系数将参与有效应力的计算,并且在渗流计算中考虑体积应变的影响,孔隙率在多孔介质骨架可压缩时用于计算骨架变形对渗流场的影响。
表3 水力学材料参数表
| 区域 | 水平渗透系数 (m/day) | 垂直渗透系数 (m/day) | 孔隙率 | Pr (MPa) | N |
|---|---|---|---|---|---|
| 砂壳 | 1 | 1 | 0.25 | 0.1 | 1.7 |
| 心墙 | 0.01 | 0.001 | 0.05 | 0.1 | 1.7 |
| 坝基1 | 0.1 | 0.0001 | 0.25 | 0.1 | 1.7 |
| 坝基2 | 0.1 | 0.01 | 0.25 | 0.1 | 1.7 |
| 坝基3 | 0.1 | 0.01 | 0.25 | 0.1 | 1.7 |
| 坝基4 | 0.1 | 0.01 | 0.25 | 0.1 | 1.7 |
-
步骤3:边界条件设置
在“边界”选项卡中,分别以表格形式输入瞬态水位变化函数。“库水位”函数时间列表输入0, 1, 4(天),水位列表输入30, 10, 0 (m),表示库水位在1天内由30米将至10米,在最后三天内放空。
下游无水,即在“地下水位”函数时间列表输入4(天),水位列表输入0(m)。
由于渗流仿真时间为4天,函数端点延拓对计算无影响。“高级设置”中上下游水位变化函数的端点延拓方式均可设置为“常数延拓”,“插值方式”选择“线性插值”。
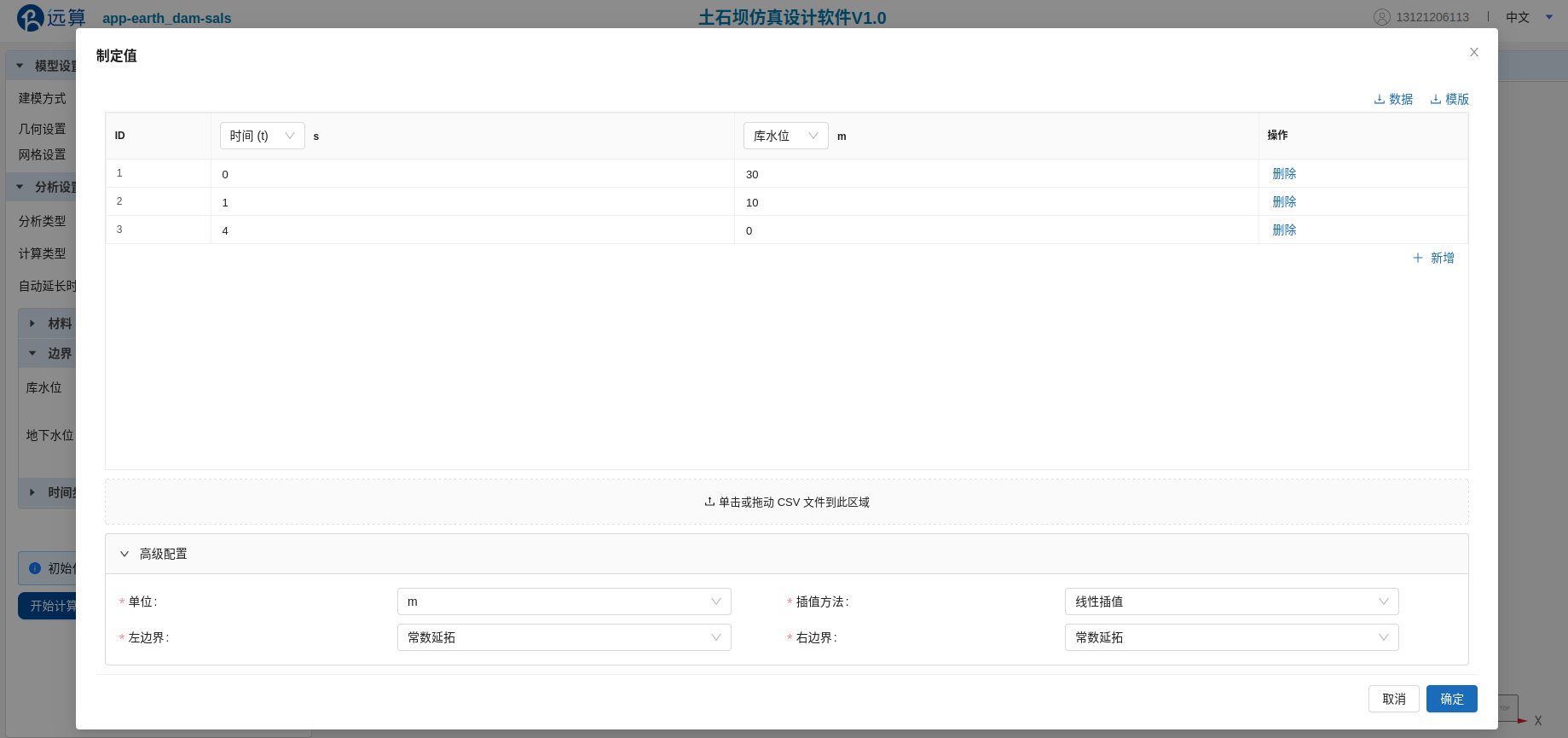
库水位函数输入界面
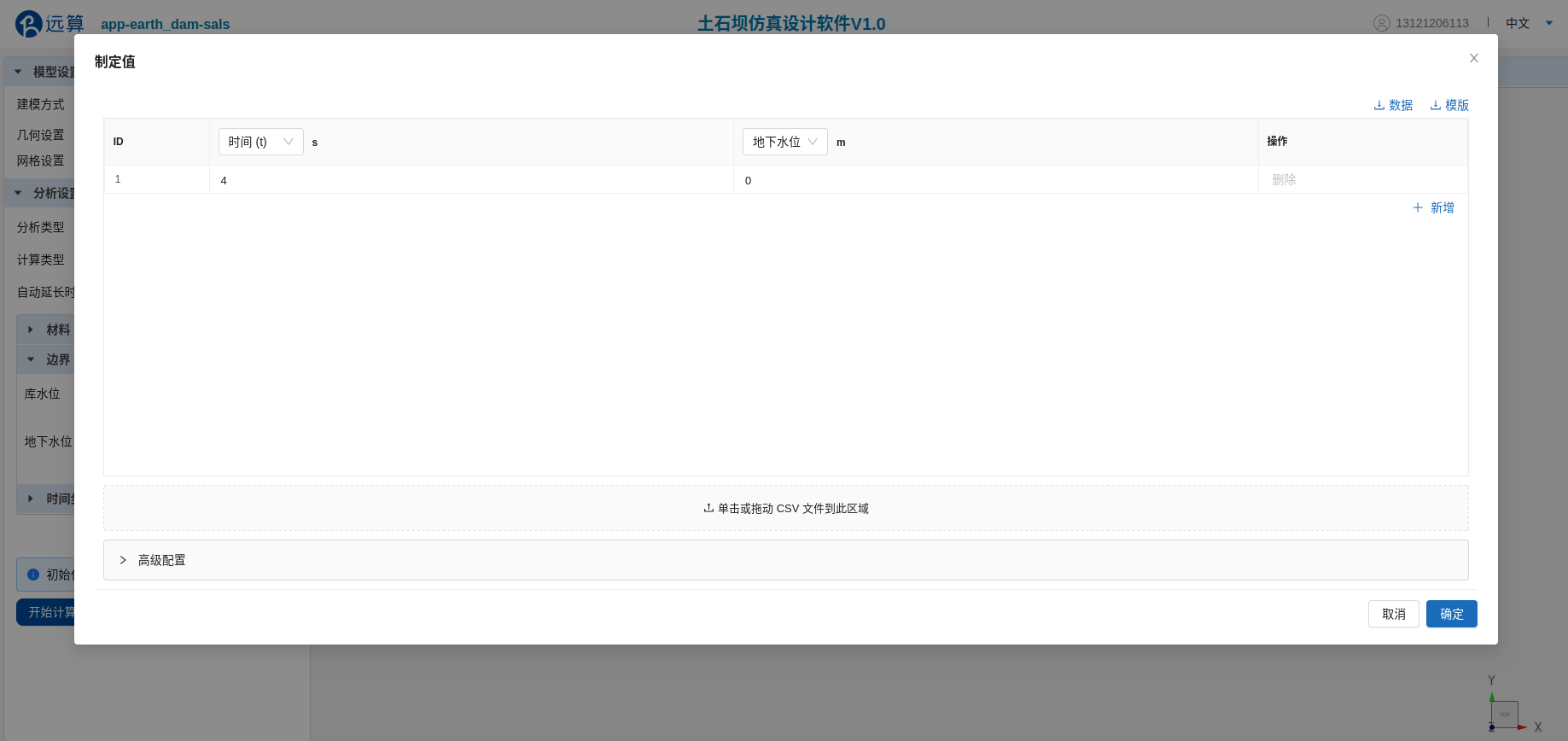
下游水位函数输入界面
-
步骤4:时间步设置
在“时间步”选项卡中设置“仿真时间”为4(天),“步数”输入常值4,表示使用均匀时间步,每步时间间隔为1天。“写入时间步”选择“按计算时间步”写入,表示结果中可查看全部4个时间步的结果。
-
步骤5:结果查看
点击“开始计算”按钮提交计算。展开右侧“计算结果”可查看计算结果。
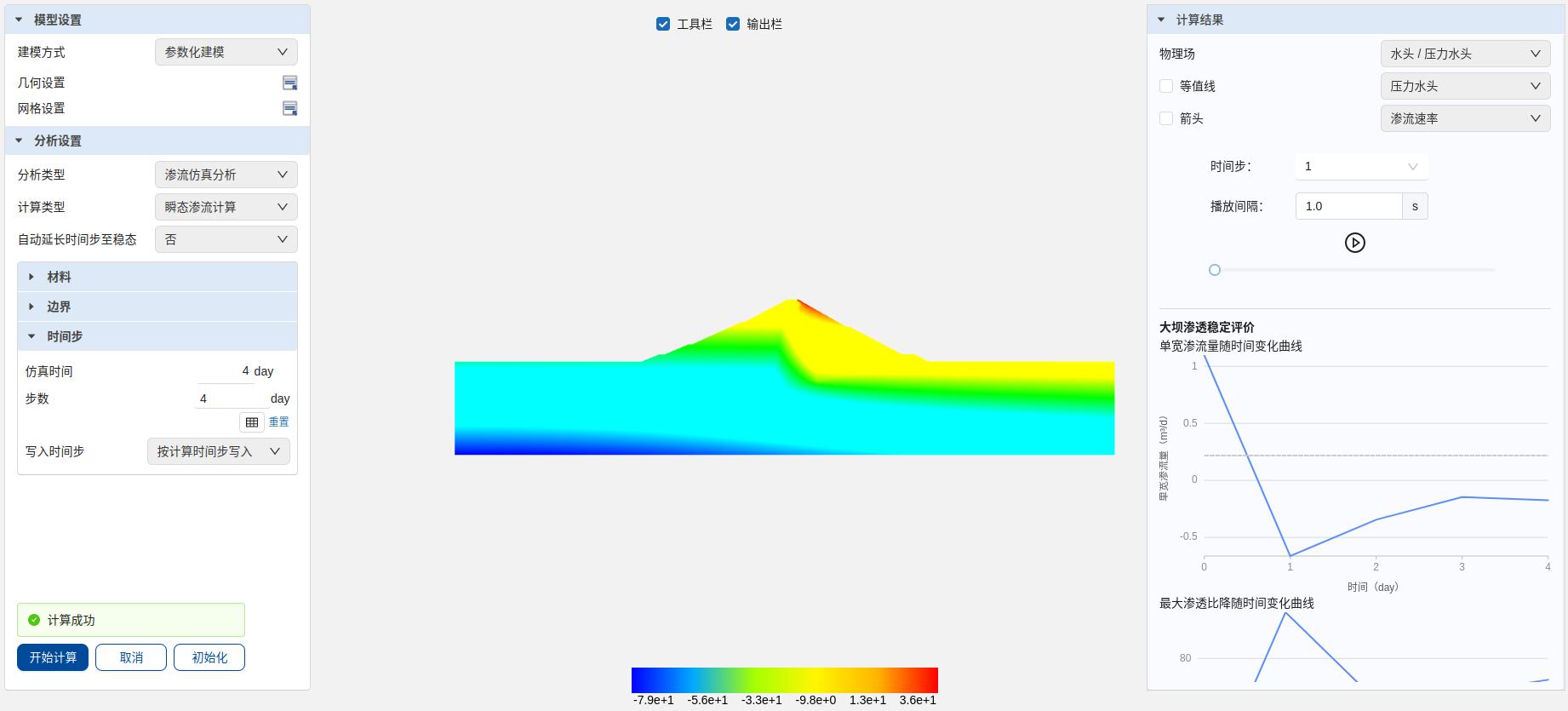
瞬态渗流计算结果查看界面
由于心墙渗透系数较低,在“物理场”选择压力水头时点击播放图标,可明显观察到上游水位骤降过程中心墙浸润线降落延迟的现象。由正常蓄水位,即初始状态的总水头等值线分布可见,总水头降落主要集中在心墙内,表明粘土心墙具有良好的挡水作用。
通过“单宽渗流量时间变化曲线”和渗流速率云图可见当库水位降落时,坝体中的水从上下游坝面同时排出。
根据大坝渗透稳定评价结果可见,水位骤降过程中,大坝最大单宽渗流量为 ,出现在初始时刻,随后由于上游库水位降落,坝体中的水从上游坝面逸出,产生约 的逸出流量,最终随着库水位与下游水位趋于一致,单宽渗流量逐渐降至0。坝体最大渗透比降约为103,出现在第1天,即水位骤降至10m时,局部集中在心墙、砂壳与第一层坝基交汇位置。突然升高的渗透比降可能导致坝体渗透变形和破坏。因此实际水库运行需避免水位快速升降。
2.3 整体稳定分析
-
步骤1:全局参数设置
在“全局设置”选项卡中将“参考标准”和“行业规范”分别选择为“中国标准(GB)”和“电力行业规范”,从而能够在整体稳定分析模块中按照NB/T 10872-2020 《碾压式土石坝设计规范》进行计算和安全校核。
-
步骤2:计算模型设置
由于大坝潜在滑动面端点所在区域未知,本案例首先采用有限元强度折减法准确计算滑动面位置,随后采用简化毕肖普法进一步复核边坡抗滑稳定性系数。
需在“分析设置”选项卡中做如下设置:
- “分析类型”:整体稳定分析
- “整体稳定分析方法”:有限元强度折减法
-
步骤3:力学材料参数设置
在“材料”选项卡中设置力学材料参数如表4所示。大坝模型除密度外近似简化为均质材料。
为了实现水力耦合计算,将“导入渗流孔隙压力场”选为“是”,同时指定导入第0步,即导入正常蓄水位工况渗流场。
表4 力学材料参数表
| 区域 | 密度(kg/m3) | 弹性模量(MPa) | 泊松比 | 摩擦角(deg) | 凝聚力(kPa) |
|---|---|---|---|---|---|
| 砂壳 | 2220 | 200 | 0.2 | 35 | 40 |
| 心墙 | 2230 | 200 | 0.2 | 35 | 40 |
| 坝基1 | 2240 | 200 | 0.2 | 35 | 40 |
| 坝基2 | 2250 | 200 | 0.2 | 35 | 40 |
| 坝基3 | 2250 | 200 | 0.2 | 35 | 40 |
| 坝基4 | 2250 | 200 | 0.2 | 35 | 40 |
-
步骤4:载荷设置
本案例不考虑力学载荷,仅在自重和渗流空隙压力作用下计算整体稳定,因此取消勾选“静水压力”载荷,使得载荷列表中没有被勾选项。
-
步骤5:评价指标设置
在电力规范中,软件同时使用单一安全系数法和分项系数法计算抗滑稳定性系数和抗滑稳定可靠度。因此需在“评价指标”选项卡中设置:
- “抗剪强度分项系数”:
- “凝聚力”:1.2
- “摩擦系数”:1.1
- “结构重要性系数”:1.0
- “设计状况系数”:1.0
- “抗剪强度分项系数”:
-
步骤6:强度折减法计算设置
在“稳定性计算参数”选项卡中设置:
- “计算区域”:下游坝坡
- “载荷列表”:不选
- “初始稳定性系数”:1.7
- “计算精度”:0.1
在“高级设置”中需确保“初始稳定性系数增量”大于等于0.1,本案例中可设置为0.1。其余参数均可保留默认值。点击“开始计算”提交计算。
-
步骤7:强度折减法计算结果查看
展开“计算结果”窗口查看结果,稳定性系数计算值为 ,且从滑动体云图上能够识别圆弧形滑动面。由于计算精度较低且非线性计算最大迭代次数和时间步划分层数较少,未观察到明显的塑性贯通区,但仍满足确定滑动面端点的需求。
由于滑弧未完全形成,此时通过强度折减法计算得到的稳定性系数远低于其真实值,这一判断可以通过稳定性系数随计算区域最大总位移的变化曲线进一步印证,当强度折减法计算收敛,同时形成完整的塑性贯通区时,稳定性系数曲线将转为水平,表示总位移的突变,表征边坡临界稳定状态。
将滑动面端点横坐标记录为86.2和152(m),作为简化毕肖普法的输入参数。该数据结果可利用简化毕肖普法计算参数设置中的鼠标拾取功能采集。
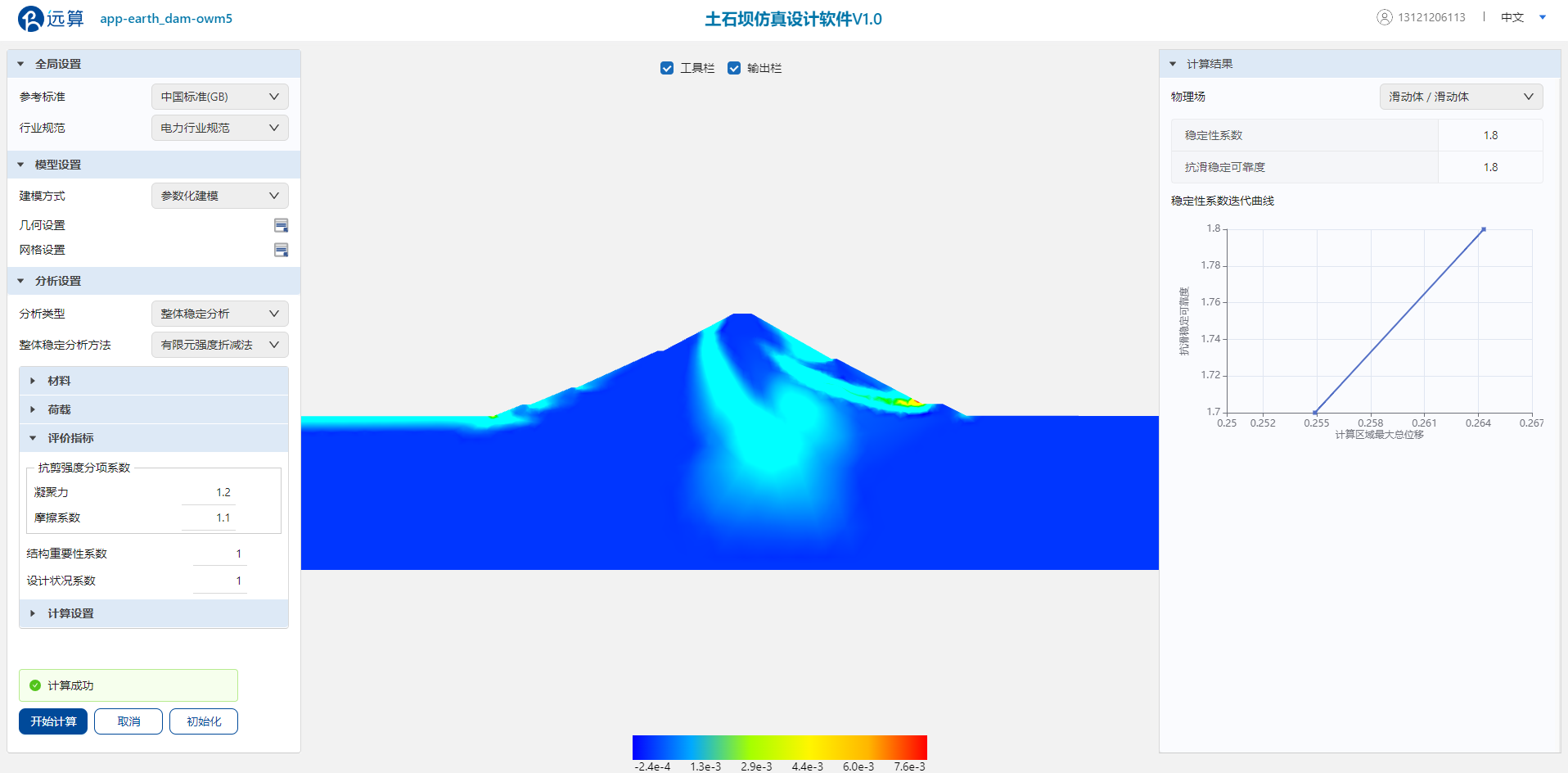
强度折减法计算结果和滑动面(积累塑性应变)云图
-
步骤8:简化毕肖普法计算设置
将“计算结果”窗口收起,将“整体稳定分析方法”切换为“简化毕肖普法”,利用鼠标拾取方法拾取强度折减法得到的塑性贯通区端点,在“稳定性计算参数”设置窗口中输入以下参数:
- “土条数量”:
- “滑动面左端点搜索范围X1”:86.2
- “滑动面左端点搜索范围X2”:86.2
- “滑动面右端点搜索范围X3”:152
- “滑动面右端点搜索范围X4”:152
同时在高级设置中,将“滑动面左端搜索点数量”和“滑动面右端搜索点数量”均设置为1,表示优化算法将在强度折减法给定的圆弧形滑动面端点条件下搜索滑动面半径使得FS最小,最小值即边坡抗滑稳定性系数。
其余参数均可保留默认值。点击“开始计算”提交计算。
-
步骤9:简化毕肖普法结果查看
展开“计算结果”窗口查看结果,稳定性系数计算值为 ,高于强度折减法计算的稳定性系数,且高于规范标准阈值1.35,因此可认为正常运用条件下游坝坡稳定。
综合考虑圆弧条分法在条间力、力和力矩平衡方程及应力重分布等方面的不合理假设,实际的下游边坡稳定性系数应位于粗略计算的强度折减法和简化毕肖普法结果之间,即FS真实值在1.8至2.7之间。
查看滑动体云图可见简化毕肖普法与强度折减法给出的下游边坡滑动体形状一致,表明滑动面搜索结果正确。简化毕肖普法同时给出了滑动面圆心坐标、滑动面半径和端点坐标等关键参数。由网格自动加密算法收敛曲线可见,最终稳定性计算结果与网格密度无关。
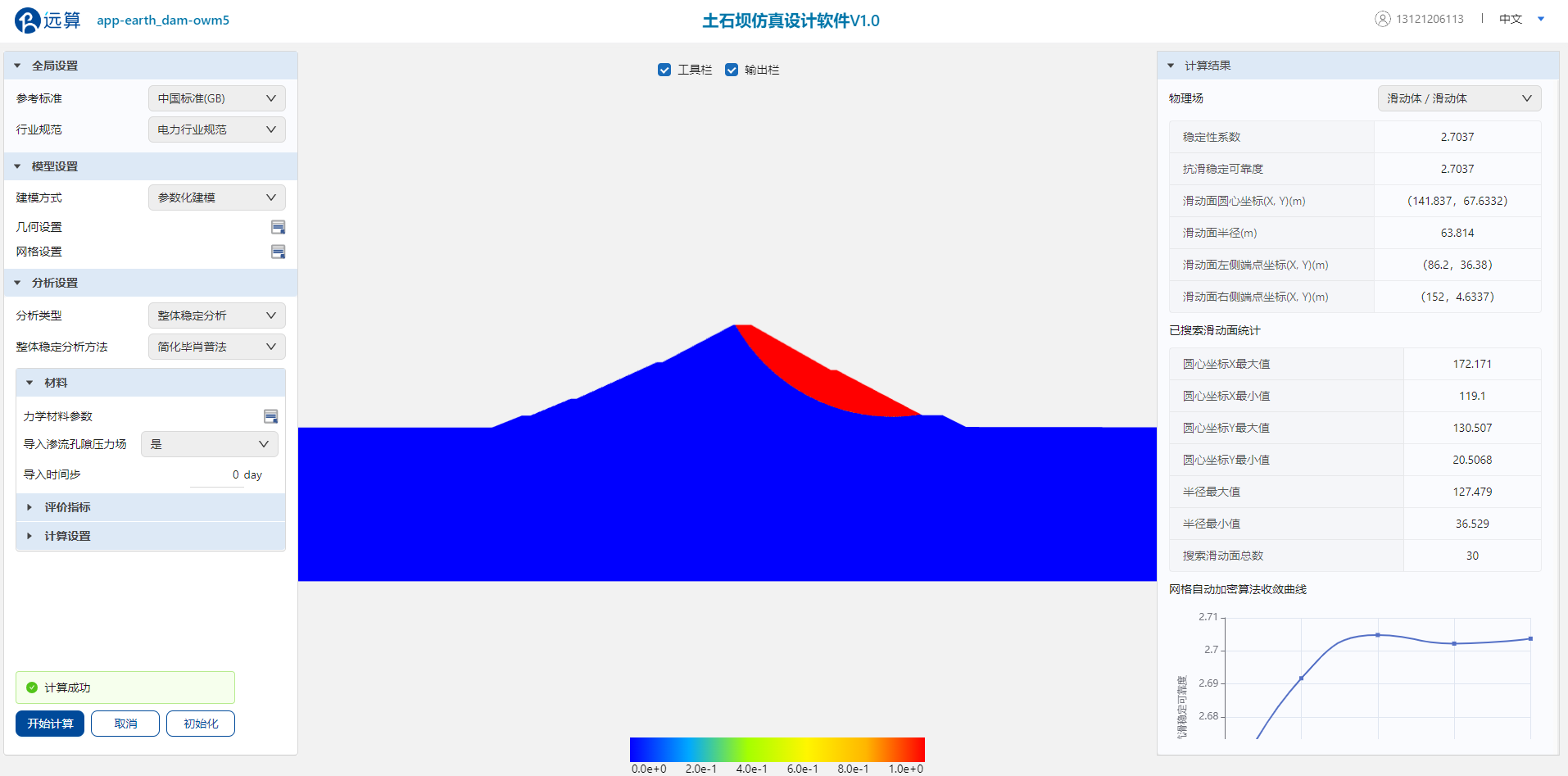
简化毕肖普法计算结果和滑动体云图
-
步骤10:地震屈服加速度计算
将“整体稳定分析方法”切换为“超载法地震屈服加速度计算”,在“荷载”选项卡中勾选“地震”,并设置“地震烈度”为VIII级。
在“稳定性计算参数”设置窗口中输入以下参数:
- “载荷列表”:不选
- “初始加速度系数”:0.5
- “计算精度”:0.1
在“高级设置”中“初始稳定性系数增量”设置为0.5。其余参数均可保留默认值。点击“开始计算”提交计算。
-
步骤11:地震屈服加速度结果查看
展开“计算结果”窗口查看结果,由滑动体云图可见明显的塑性贯通区,由上游坝面靠近坝顶位置到下游坝面最后一级马道。计算得到屈服加速度系数 。
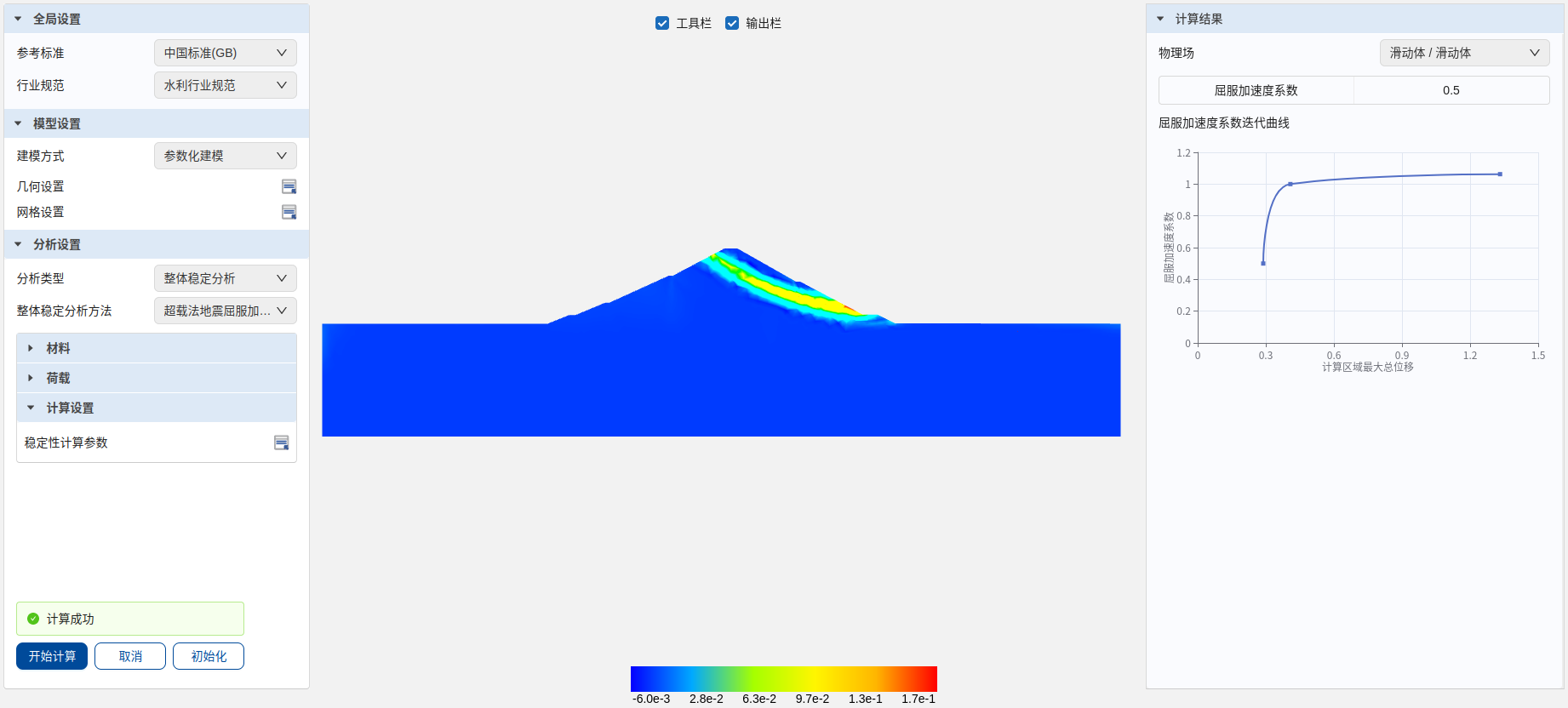
超载法地震屈服加速度计算结果
2.4 动力学时程分析
-
步骤1:材料参数设置
动力学时程分析除力学材料参数外,需设置阻尼参数。力学参数同样使用表4中定义的材料参数,随后在“阻尼”设置窗口将所有区域“模态阻尼”设置为0.02,“瑞利阻尼”设置为:
在实际计算中使用“瑞利阻尼”,在“计算设置”选项卡中“阻尼”选项设置。
-
步骤2:地震动输入设置
点击“上传”按钮将El_Centro地震加速度谱导入,导入后即可在窗口上部曲线图预览加速度谱时域波形。
在“加速度谱修正”设置表中将X、Y方向加速度的放大倍数分别设置为10和50,滤波截至频率分别设置为0.05Hz。
为了加快后处理速度,在“写入时间步设置”中选择“等间隔步数写入”,并将“写入间隔步数”设置为10步。
在“地震动输入算法”选项卡中选择“平面波模型”,同时设置“地震波类型”为“P波”,即由坝基边界竖直向上传播的压缩波。
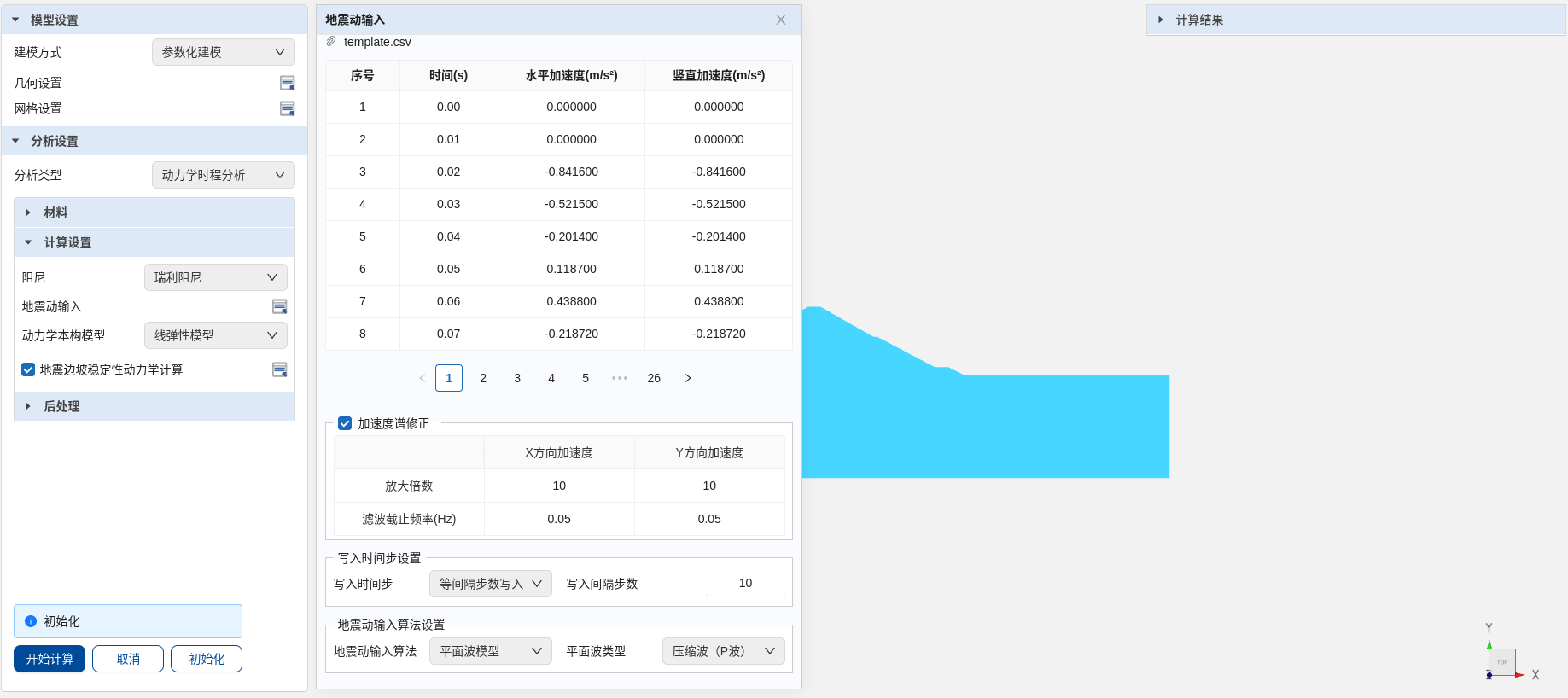
地震动输入设置窗口
-
步骤3:地震边坡稳定动力学计算设置
为了计算地震永久变形,勾选“地震边坡稳定性动力学计算”,并在设置窗口中选择“端点坐标输入”,根据超在法屈服加速度的计算结果,设置参数如下:
- “滑动面半径”:97.7m
- “滑动面左端点X坐标X1”:80.05m
- “滑动面右端点X坐标X2”:150m
- “地震屈服加速度系数”:0.1m/s2
由于计算使用了瑞利阻尼,为了观察到明显的边坡永久变形,此处将屈服加速度计算结果折减10倍作为屈服加速度系数。
-
步骤4:添加兴趣点
在“后处理”选项卡使用默认的两个兴趣点。点击“开始计算”按钮提交计算。
-
步骤5:结果查看
展开“计算结果”窗口,通过切换“物理场”查看2s地震时间历程中最大剪应变云图,坝体最大剪应变约为1e-2。切换“曲线图”查看“地震边坡稳定”计算结果,可见边坡滑动体永久变形量约为0.52m。
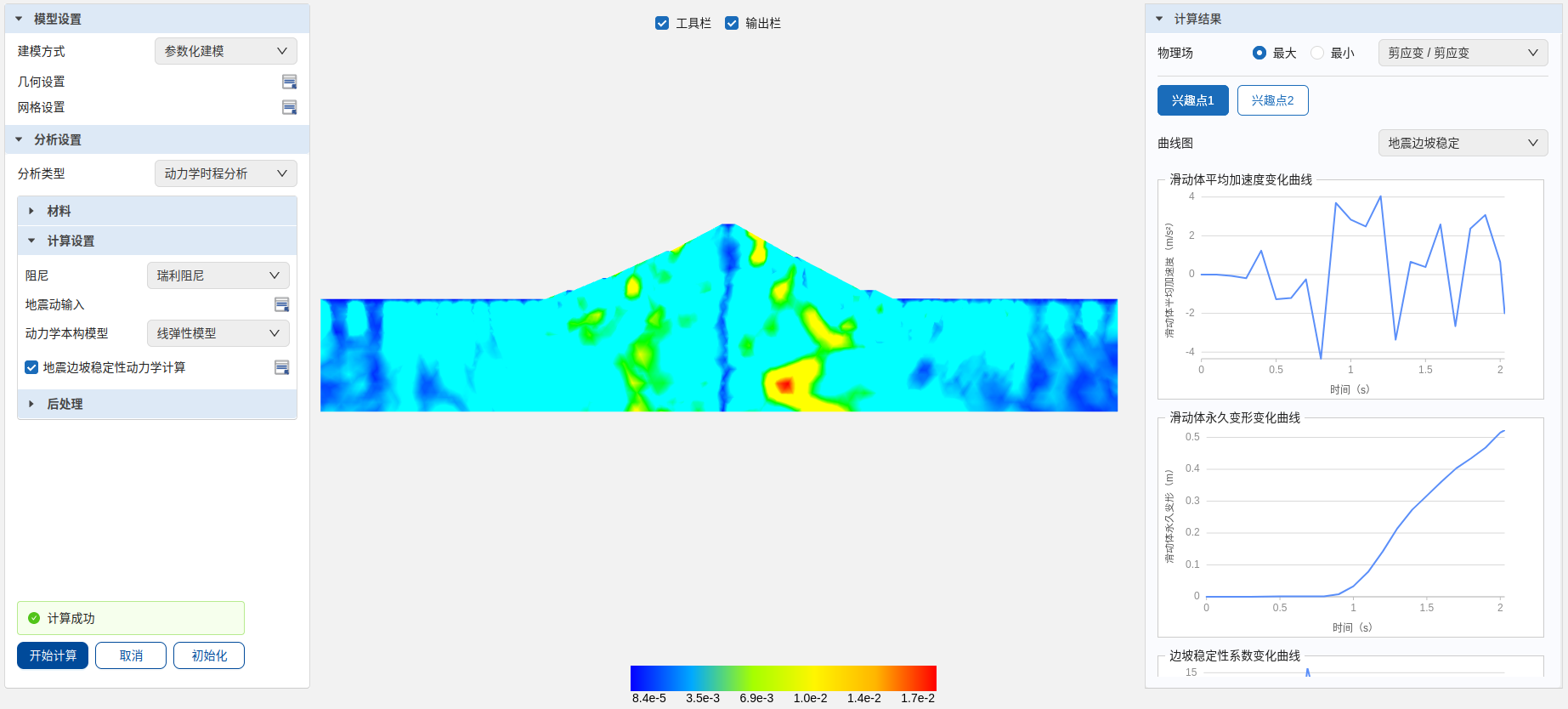
动力学时程分析计算结果
